Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
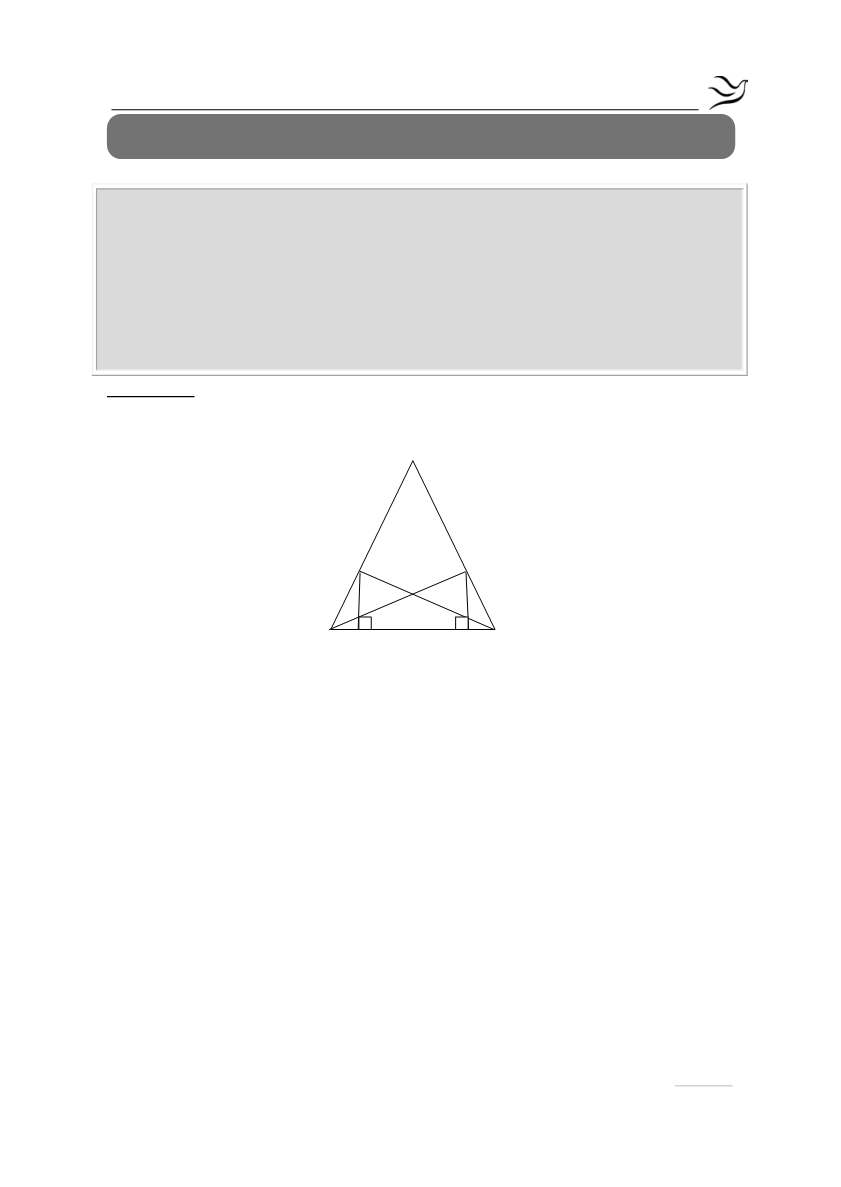
Δίνεται ισοσκελές τρίγωνο ΑΒΓ (ΑΒ = ΑΓ) και οι διχοτόμοι του ΒΔ και ΓΕ. Αν
ΕΗ ΒΓ
⊥
και
ΔΖ ΒΓ
⊥
, να αποδείξετε ότι:
α) τα τρίγωνα ΒΓΔ και ΓΒΕ είναι ίσα
(Μονάδες 13)
β) ΕΗ = ΔΖ.
(Μονάδες 12)
Απάντηση:
α) Αφού το τρίγωνο ΑΒΓ είναι ισοσκελές με ΑΒ=ΑΓ θα είναι και
Γ Β
=
.
Επομένως, τα τρίγωνα ΒΓΔ και ΓΒΕ είναι ίσα γιατί
•
ΒΓ κοινή
•
ΓΒΔ ΒΓΕ
=
ως μισά ίσων γωνιών και
•
Γ Β
=
.
β) Από τη σύγκριση των τριγώνων ΒΓΔ και ΓΒΕ προκύπτει ότι ΓΔ=ΒΕ. Επομένως,
τα τρίγωνα ΒΕΗ και ΓΔΖ είναι ίσα γιατί
•
0
ΕΗΒ ΔΖΓ 90
= =
•
ΓΔ=ΒΕ
•
Β Γ
=
.
Συνεπώς, ΕΗ = ΔΖ.
Α
Ε
Δ
Β
Γ
Ζ
Η
ΘΕΜΑ 2824
7









