Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

85 / 146

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου
84
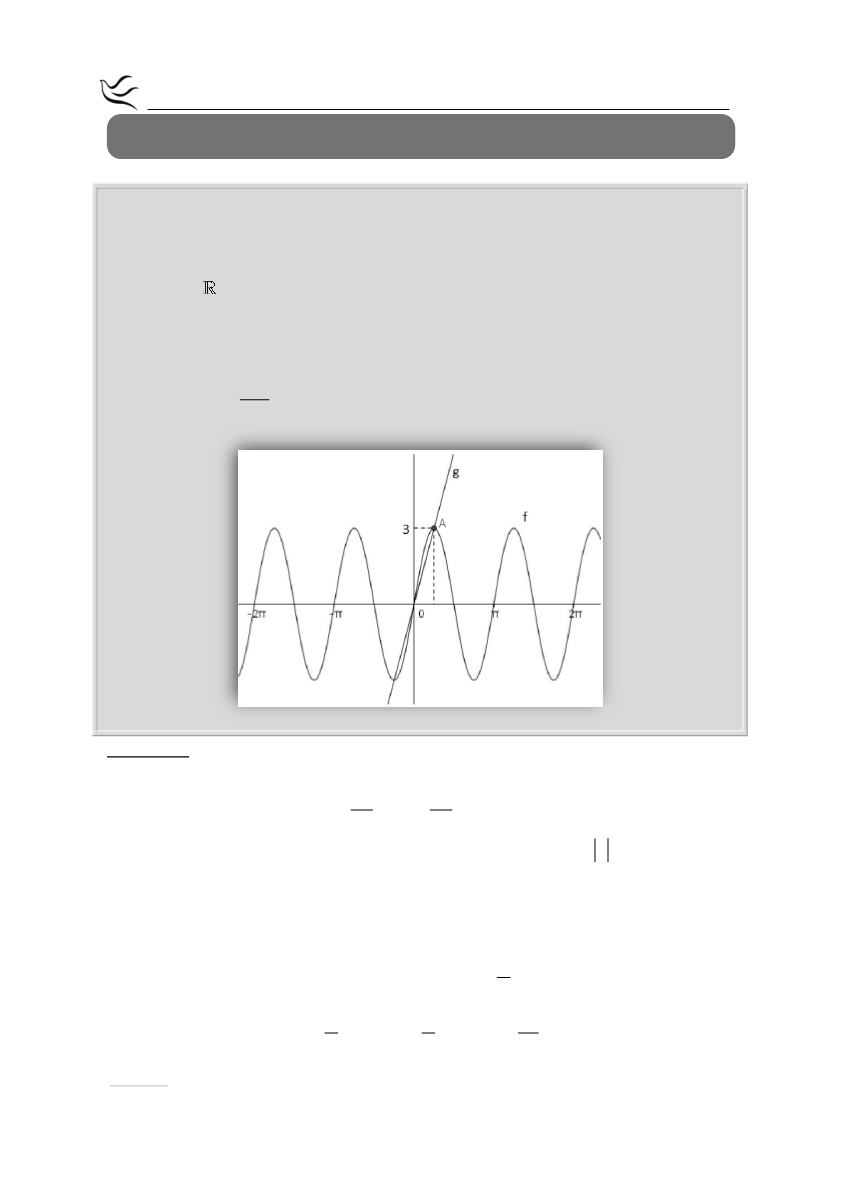
Στο παρακάτω σχήμα δίνεται η γραφική παράσταση της συνάρτησης
  g x αx β  , όπου α, β πραγματικοί αριθμοί και της συνάρτησης
    f x ρημ ωx , όπου ω > 0 και ρ > 0. Και οι δύο συναρτήσεις έχουν πεδίο
ορισμού το . Επίσης η f έχει μέγιστο 3.
α. Να αποδείξετε ότι ρ 3 και ω 2 . (Μονάδες 5)
β. Να βρείτε τα α και β. (Μονάδες 10)
γ. Να βρείτε γραφικά, το πλήθος των λύσεων της εξίσωσης
  12x
3ημ 2x 0
π
  . (Μονάδες 10)
Απάντηση:
α. Βλέπουμε ότι η συνάρτηση έχει περίοδο Τ π άρα:
2π 2π
Τ π ω 2
ω ω
    
Επίσης, η συνάρτηση έχει μέγιστο 3 που σημαίνει ότι ρ 3 και εφόσον
έχουμε ότι ρ 0 καταλήγουμε ότι ρ 3 .
β. Παρατηρούμε από τη γραφική παράσταση ότι η g C διέρχεται από την
αρχή των αξόνων άρα β 0 .
Επιπλέον η g C διέρχεται από το σημείο
π
Α ,3
4
 
 
 
άρα:
π π 12
g 3 α 3 α
4 4 π
 
     
 
 
ΘΕΜΑ 68. 4-20921