Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

84 / 146

83
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
α. Να αποδείξετε ότι
π
ω
2
 . (Μονάδες 5)
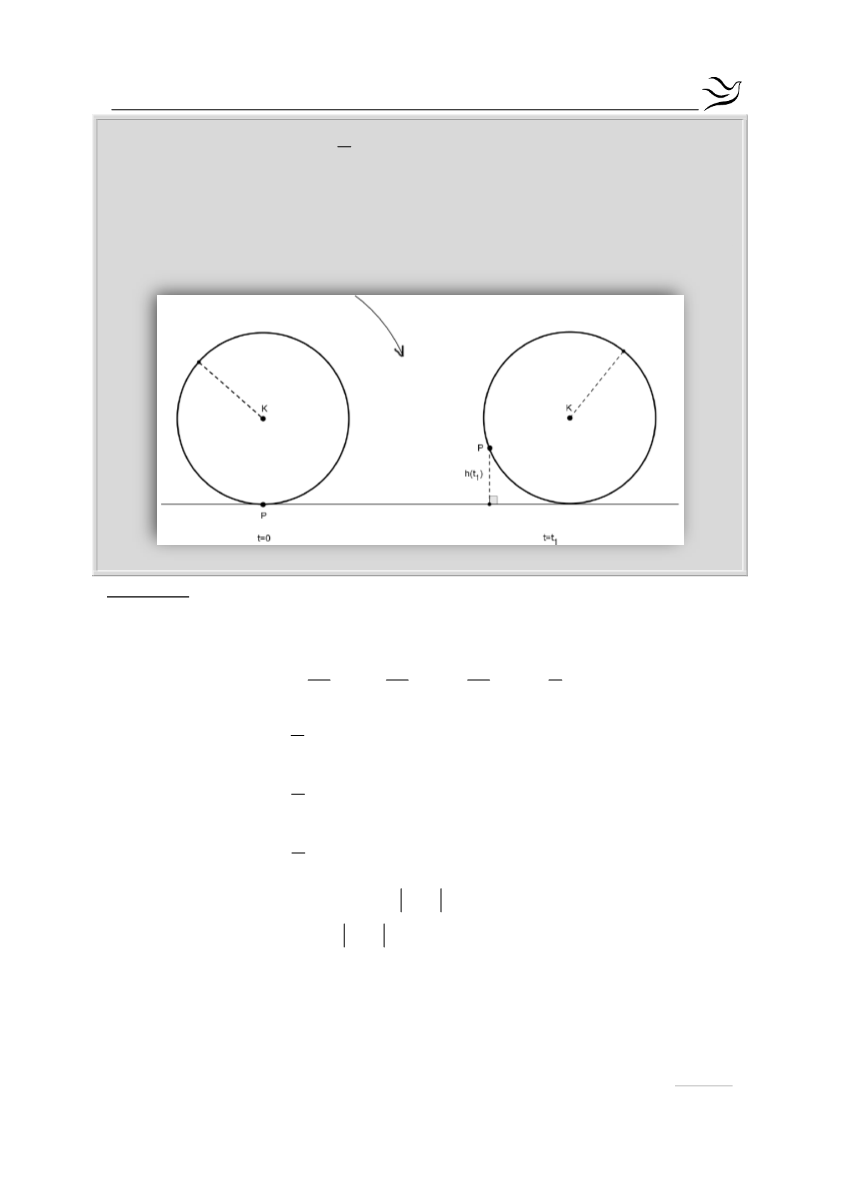
β. Να προσδιορίσετε την απόσταση του Ρ από την επιφάνεια τις στιγμές:
1 t 1sec , 2 t 2sec και 3 t 7sec  . (Μονάδες 6)
γ. Να βρείτε την μέγιστη και την ελάχιστη τιμή της h . (Μονάδες 5)
δ. Να προσδιορίσετε την ακτίνα της ρόδας. (Μονάδες 9)
Απάντηση:
α. Εφόσον για να κάνει μία πλήρη περιστροφή χρειάζεται 4sec έχουμε ότι
T 4 . Συνεπώς:
2π 2π 2π π
T 4 ω ω
ω ω 4 2
      
β.    
π
h 1 0,2συν 1 0,2 h 1 0,2
2
 
     
 
 
   
π
h 2 0,2συν 2 0,2 h 2 0, 4
2
 
     
 
 
   
π
h 7 0,2συν 7 0,2 h 7 0,2
2
 
     
 
 
γ. Η μέγιστη τιμή θα είναι: max h 0,2 0,2 0,4    
και η ελάχιστη: max h 0,2 0,2 0     
δ. Από την διαφορά max min h h  συμπεραίνουμε ότι η διάμετρος της ρόδας
είναι 0,4m , άρα η ακτίνα είναι 0,2m .