Αλγεβρα A' Λυκείου (Τράπεζα Θεμάτων)

237 / 240

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου
236
  2 2 Δ 0 4 λ 4λ 5 0 λ 4λ 5 0 λ 5 ή λ 1.             
γ) Η δοθείσα εξίσωση έχει δύο ρίζες άνισες αν και μόνο αν ισχύει
  2 2 Δ 0 4 λ 4λ 5 0 λ 4λ 5 0          .
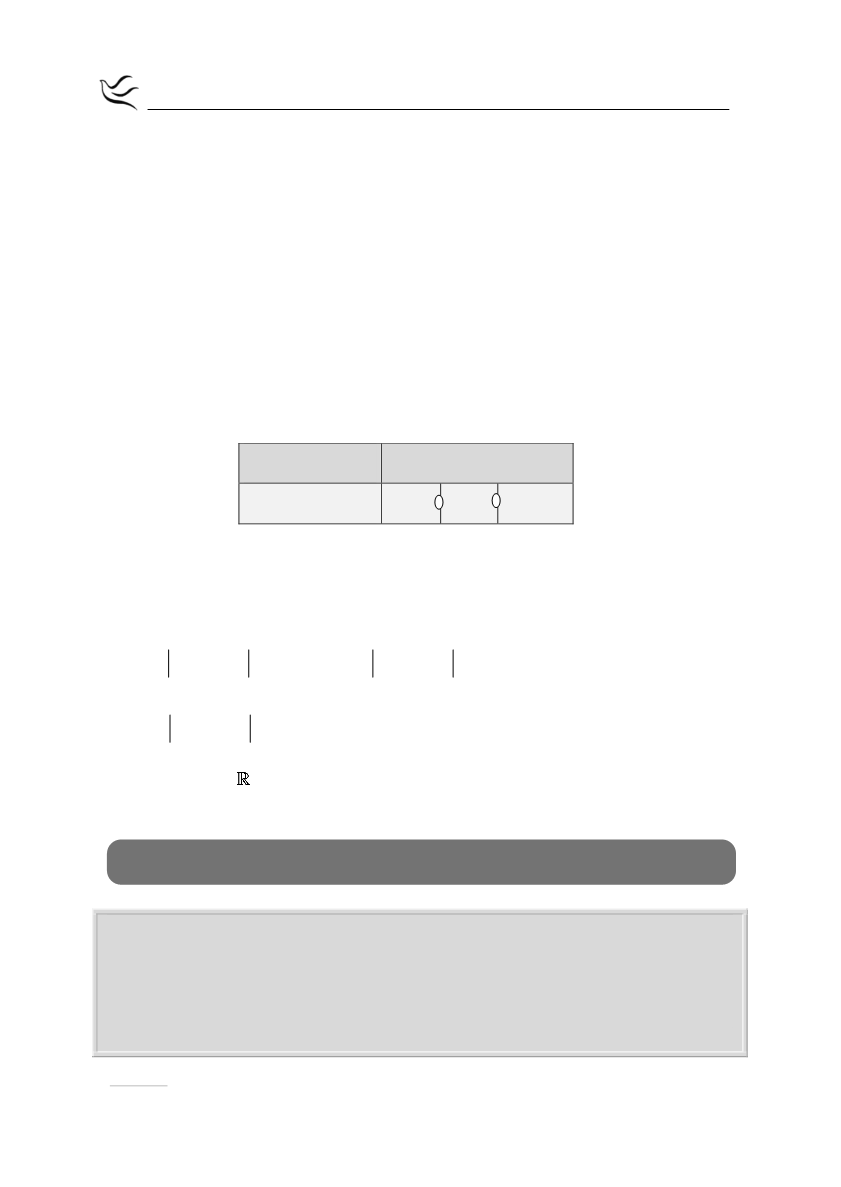
Οι ρίζες και το πρόσημο του τριωνύμου 2
λ 4λ 5   φαίνονται στον
παρακάτω πίνακα.
Επομένως,     2
λ 4λ 5 0 λ , 1 5, .         
δ) Έχουμε
   
2 2 2 2
2 2 2 2
λ 4λ 5 4λ λ 5 λ 4λ 5 λ 4λ 5
λ 4λ 5 λ 4λ 5 λ 4λ 5 0 4 λ 4λ 5 0 Δ 0.
           
                
Επίσης,   λ 1, 5 .    Δηλαδή Δ 0. Από τα παραπάνω συμπεραίνουμε
ότι Δ 0 , δηλαδή ότι η δοθείσα εξίσωση δεν έχει πραγματικές ρίζες.
Δίνεται η συνάρτηση f με
x 2, x 0
f(x)
x 2, x 0
   
 
 

α) Να βρείτε το σημείο της γραφικής παράστασης f C της f με τον άξονα y y
( Μονάδες 3)
ΘΕΜΑ 4-4657
λ  1  5 
2 λ 4λ 5     