45
Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
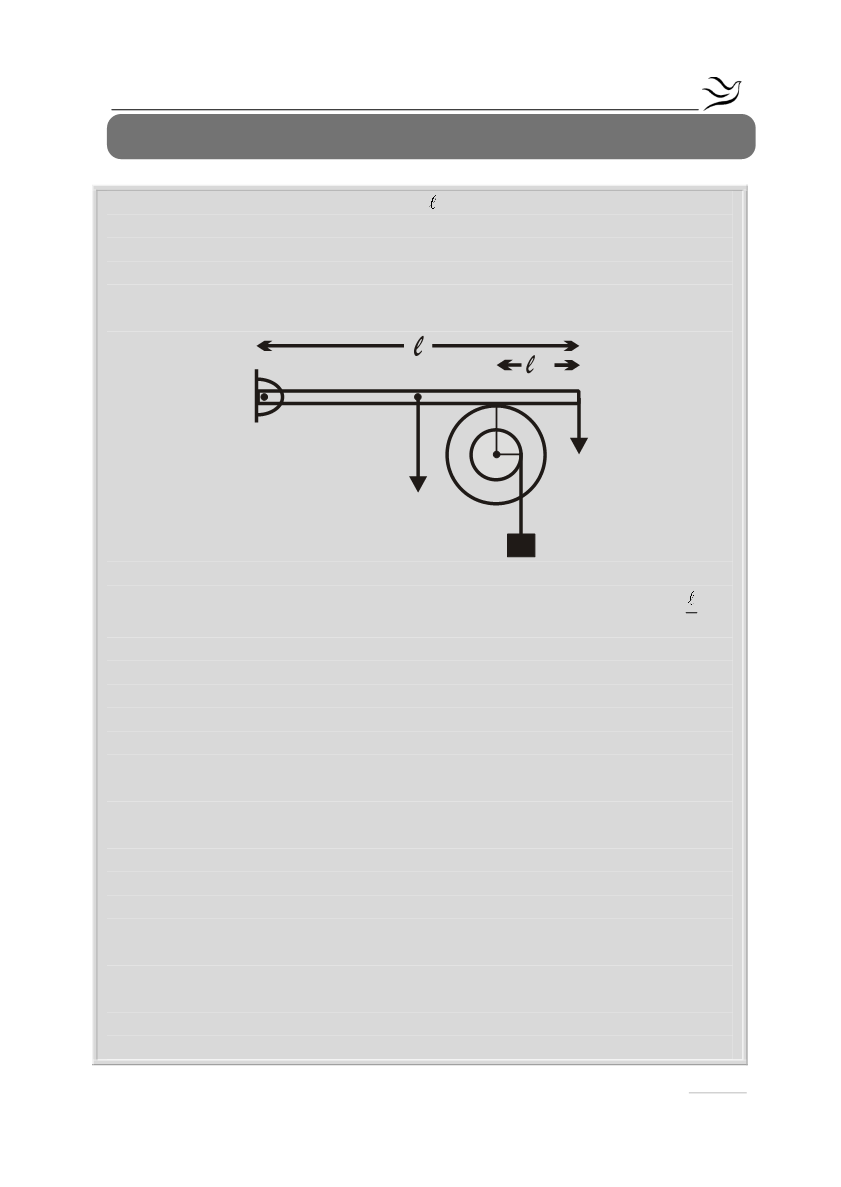
Άκαμπτη ομογενής ράβδος ΑΓ με μήκος και μάζα Μ = 3kg έχει το άκρο της Α
αρθρωμένο και ισορροπεί οριζόντια. Στο άλλο άκρο Γ ασκείται σταθερή
κατακόρυφη δύναμη F μέτρου 9Ν, με φορά προς τα κάτω. Η ράβδος ΑΓ
εφάπτεται στο σημείο Β με στερεό που αποτελείται από δύο ομοαξονικούς
κυλίνδρους με ακτίνες R
1
= 0,1m και R
2
= 0,2m, όπως φαίνεται στο σχήμα.
Η απόσταση του σημείου επαφής Β από το άκρο Γ της ράβδου είναι
4
. To
στερεό μπορεί να περιστρέφεται χωρίς τριβές, σαν ένα σώμα γύρω από
σταθερό οριζόντιο άξονα που περνάει από το κέντρο του. Ο άξονας
περιστροφής συμπίπτει με τον άξονα συμμετρίας των δύο κυλίνδρων. Η ροπή
αδράνειας του στερεού ως προς τον άξονα περιστροφής είναι Ι = 0,09 kgm
2
.
Γύρω από τον κύλινδρο ακτίνας R
1
είναι τυλιγμένο αβαρές και μη εκτατό νήμα
στο άκρο του οποίου κρέμεται σώμα μάζας m = 1kg.
α.
Να υπολογίσετε την κατακόρυφη δύναμη που δέχεται η ράβδος στο σημείο
Β από το στερεό. (Μονάδες 6)
β.
Αν το σώμα μάζας m ισορροπεί, να βρείτε το μέτρο της δύναμης της
στατικής τριβής μεταξύ της ράβδου και του στερεού. (Μονάδες 6)
γ.
Στο σημείο επαφής Β μεταξύ ράβδου και στερεού ρίχνουμε ελάχιστη
ποσότητα λιπαντικής ουσίας έτσι, ώστε να μηδενιστεί η τριβή χωρίς να
επιφέρει μεταβολή στη ροπή αδράνειας του στερεού. Να υπολογίσετε το
μέτρο της ταχύτητας του σώματος μάζας m, όταν θα έχει ξετυλιχθεί νήμα
μήκους 0,5m. Να θεωρήσετε ότι το νήμα ξετυλίγεται χωρίς να ολισθαίνει στον
εσωτερικό κύλινδρο. (Μονάδες 6)
A
W
F
B
Γ
m
/4
R
2
1
R
ΘΕΜΑ 4
ο
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2006









