Φυσική Γ' Λυκείου

187 / 290

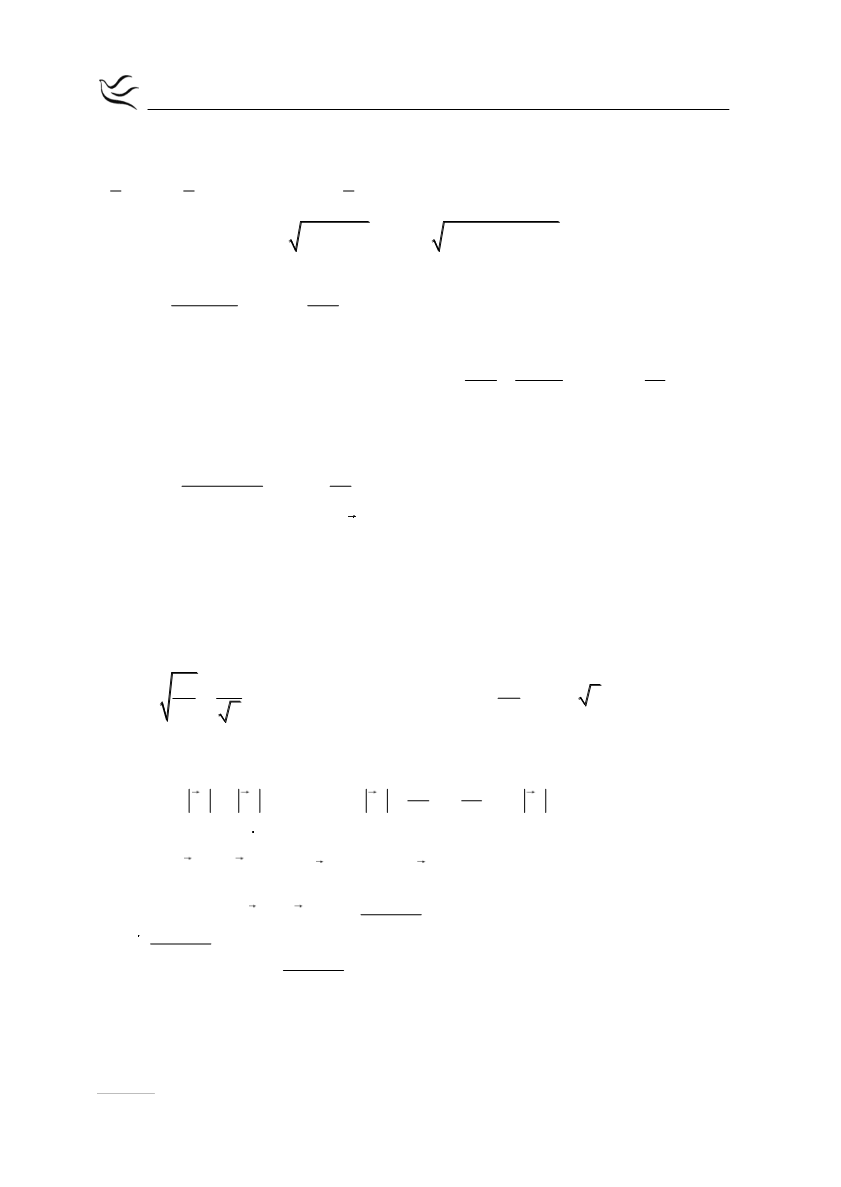
Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης
186
Για την ταχύτητα υ2 με εφαρμογή του Θ.Μ.Κ.Ε. (  Ζ Β(λ.π.)) για τη κίνηση του
σώματος Σ2 πριν την κρούση έχουμε:
2
2 2 Z B 2 2
2 2 2 0 m g 2 2 0 2
1 1 1
m υ m υ W m (υ υ ) m gh
2 2 2

      
       2 2 2
2 0 2 0 υ υ 2gh υ υ 2gh       2
2 2 υ 12 2 10 2,2 m/ s υ 10m/ s
Με αντικατάσταση στην εξίσωση (1) προκύπτει
  
 2 2
340 340
f 700 Ηz 700 Hzήf 680Hz
340 10 350
β. Για την επιμήκυνση Δl, του ελατηρίου στη Θ.Ι. (Β) του σώματος Σ1 έχουμε:
1
(B) ελ(Β) 1 1 1 1 1
m g 17 10 17
ΣF 0 F m g 0 kΔl m g Δl m Δl m
k 60 6

          
Στη Θ.Ι. (0) του συσσωματώματος ισχύει:
       
(0) ελ(0) 1 2 2 1 2 ΣF o F (m m )g 0 kΔl (m m )g (2)

   1 2
2 2
(m m )g 20
και Δl Δl m
k 6
Για την αλγεβρική τιμή της ΣF που ασκείται στο συσσωμάτωμα στη θέση Β
(μπορεί να θεωρηθεί τυχαία θέση) με θετική φορά αυτή της απομάκρυνσης
έχουμε:
       
          
ελ 1 2 2 0 1 2
2 0 2 0 0
ΣF F (m m )g k(Δl y ) (m m )g
ΣF kΔl ky kΔl ΣF ky ,y y,ΣF ky (3)
Σύμφωνα με την εξίσωση (3) το συσσωμάτωμα εκτελεί Α.Α.Τ με D=k, περίοδο
  1 m 2π
T 2π sec
k 3
και γωνιακή συχνότητα   
2π
ω ω 3 rad/ s
T
.
Για το μέτρο της απομάκρυνσης του συσσωματώματος αμέσως μετά την
κρούση έχουμε:
         
2 1 0 0 2 1 0 0
20 17
Δl Δl y y Δl Δl y m m y 0,5m
6 6
Για την ταχύτητα Κ υ του συσσωματώματος αμέσως μετά την κρούση έχουμε:
    

 
 

  
  
 
 

(Β) (λ.π.) (α.μ.) 2 2 1 2 K
2
K 2
1 2 2
K
2 1 2
K 2 Κ
1 2
Α.Δ.Ο. : Ρ Ρ m υ (m m )υ
m
υ υ ,αφού 0
m m
m
υ
m m m
υ υ υ 1,5m/ s
m m
Για το πλάτος της Α.Α.Τ. του συσσωματώματος έχουμε: