117
Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
1
1 1
τελ.
τελ.
1
5 I
4
I ω ω ω ω
4
5
(1)
Άρα η τελική στροφορμή του δίσκου Δ
1
έχει μέτρο:
(1)
1(τελ.)
1 τελ.
1(τελ.)
1
1
1
4 4
L
I ω L
I
ω L
5 5
(2)
Οπότε:
1 1
1
1(τελ.)
1(arx.)
1
1 1 1
4
I ω L
ΔL L
L
I ω I ω
5
5 5
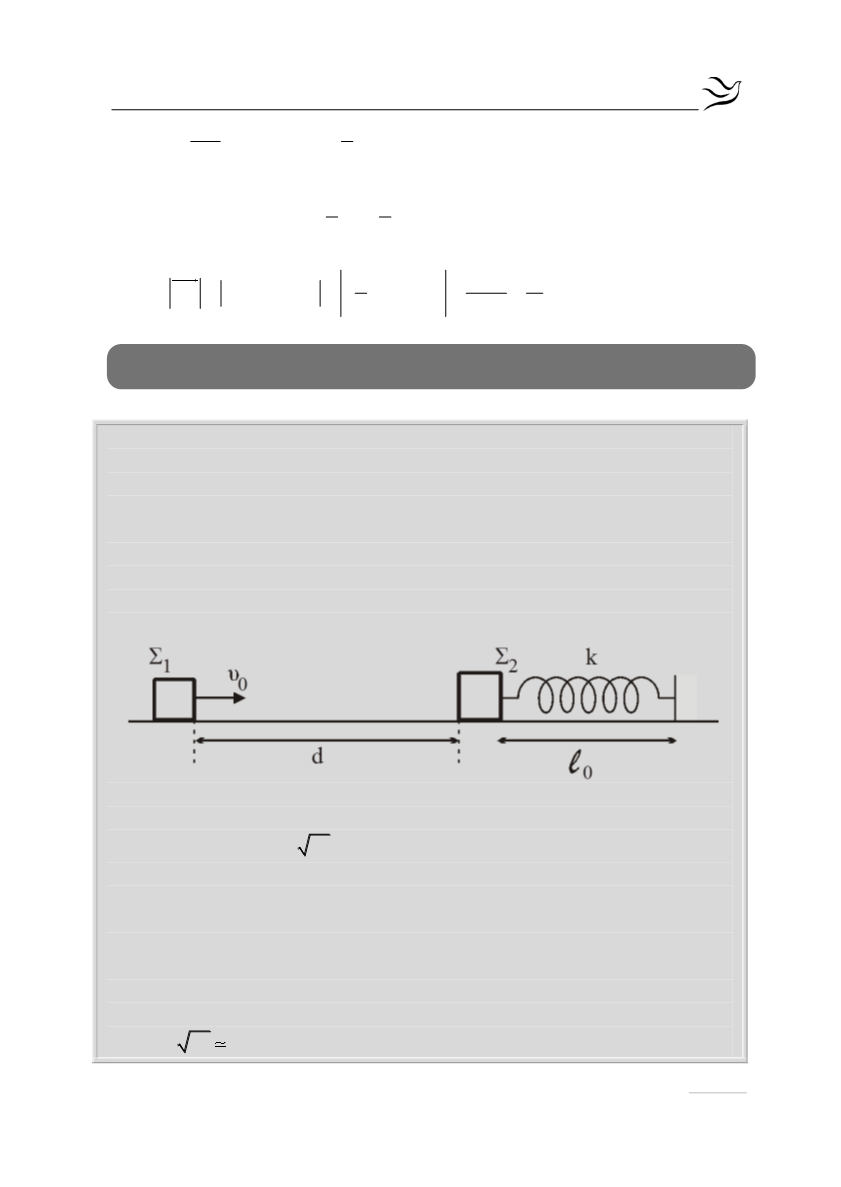
Σώμα
Σ
1
με μάζα
m
1
κινείται σε οριζόντιο επίπεδο ολισθαίνοντας προς άλλο
σώμα
Σ
2
με μάζα
m
2
= 2
m
1
, το οποίο αρχικά είναι ακίνητο. Έστω
υ
0
η
ταχύτητα που έχει το σώμα
Σ
1
τη στιγμή
t
0
= 0 και ενώ βρίσκεται σε απόσταση
d
= 1 m από το σώμα
Σ
2
. Αρχικά, θεωρούμε ότι το σώμα
Σ
2
είναι ακίνητο πάνω
στο επίπεδο δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου με αμελητέα
μάζα και σταθερά ελατηρίου
k
, και το οποίο έχει το φυσικό του μήκος ℓ
0
. Το
δεύτερο άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο τοίχο, όπως
φαίνεται στο σχήμα:
Αμέσως μετά τη κρούση, που είναι κεντρική και ελαστική, το σώμα Σ
1
αποκτά
ταχύτητα με μέτρο
'
1
υ 10 m/s
και φορά αντίθετη της αρχικής ταχύτητας.
Δίνεται ότι ο συντελεστής τριβής ολίσθησης των δύο σωμάτων με το οριζόντιο
επίπεδο είναι μ = 0,5 και ότι η επιτάχυνση της βαρύτητας είναι g = 10 m/s
2
.
Γ1.
Να υπολογίσετε την αρχική ταχύτητα υ
0
του σώματος Σ
1
. (Μονάδες 6)
Γ2.
Να υπολογίσετε το ποσοστό της κινητικής ενέργειας που μεταφέρθηκε από
το σώμα Σ
1
στο σώμα Σ
2
κατά την κρούση. (Μονάδες 6)
Γ3.
Να υπολογίσετε το συνολικό χρόνο κίνησης του σώματος Σ
1
από την αρχική
χρονική στιγμή t
0
μέχρι να ακινητοποιηθεί τελικά. (Μονάδες 6)
Δίνεται:
10 3,2
ΘΕΜΑ Γ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2013









