Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης
106
2
2
2
δ cm
1
1
I I
M M M
2 12
4
2
2
δ
4M M
I
.
12 3
Άρα:
2
2
συστ
δ σφ
M
I
I I
m
3
2
2
2
συστ
M M 5M
I
3 2 6
2
2
2
συστ
συστ
5 6 9 10
I
I
45 10 kg m .
6
Γ2.
Ισχύει:
1
π
120
π
W τ θ F
W 3 10
W 18 J.
2
π
2
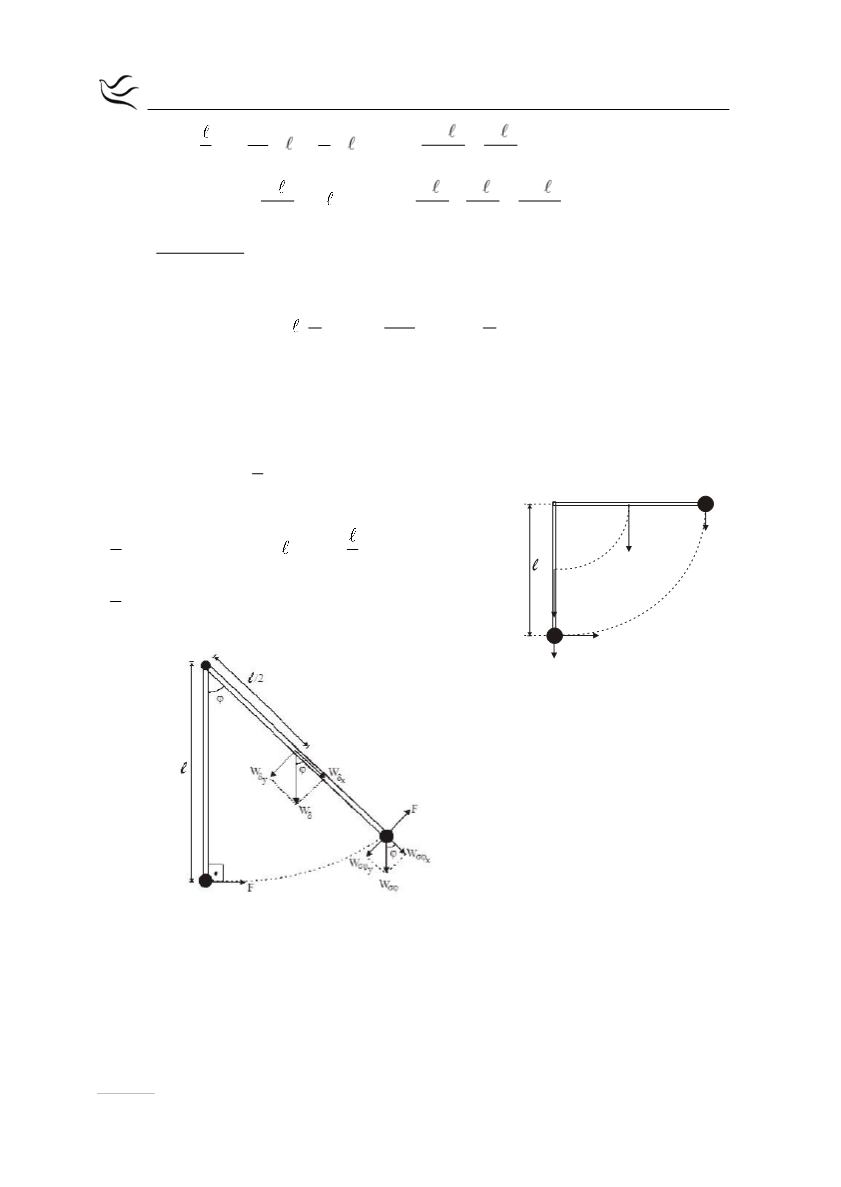
Γ3.
Εφαρμόζουμε Θ.Μ.Κ.Ε. κατά την περιστροφή του συστήματος από τη θέση
Α στη θέση Γ.
(σφ)
(δ)
2
τελ
αρχ
συστ
F
βαρ
βαρ
1
K K ΣW I
ω W W W
2
2
1
0,45 ω 18 m g M g
2
2
2
1
0,45 ω 18 3 10 0,3 6 10 0,15 ω 0
2
Γ4.
Καθώς η ράβδος ανεβαίνει, αυξάνεται η ροπή του βάρους ενώ η ροπή της F
παραμένει σταθερή. Η ράβδος θα επιταχύνεται, όσο η ροπή της F είναι
μεγαλύτερη.
Μέγιστη κινητική ενέργεια έχουμε όταν ω = ω
max
δηλαδή τη στιγμή που
α
γων
= 0. Όμως
συστ γων
Στ I
α Στ 0.
Αμέσως μετά, η ροπή του βάρους θα γίνει μεγαλύτερη από την ροπή της F και η
A
F
m.g
M.g
( )cm
Γ
m.g
( )cm
M.g









