105
Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Ομογενής και ισοπαχής δοκός (
ΟΑ
), μάζας
M
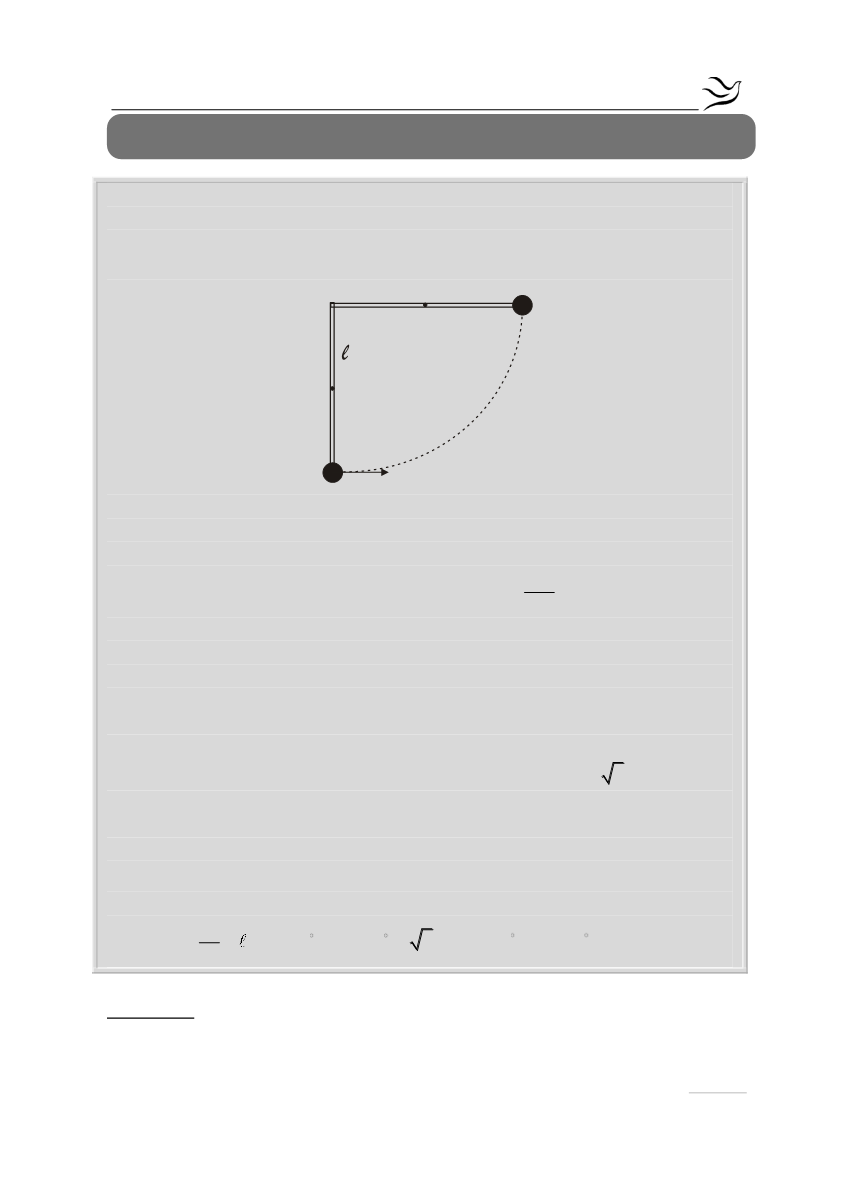
= 6 kg και μήκους ℓ = 0,3 m,
μπορεί να στρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο γύρω από οριζόντιο
άξονα που περνά από το ένα άκρο της
Ο
. Στο άλλο της άκρο
Α
υπάρχει
στερεωμένη μικρή σφαίρα μάζας
m M/ 2
.
Γ1.
Βρείτε την ροπή αδράνειας του συστήματος δοκού-σφαίρας ως προς τον
άξονα περιστροφής του. (Μονάδες 6)
Ασκούμε στο άκρο
Α
δύναμη, σταθερού μέτρου
120
F
Ν
π
, που είναι συνεχώς
κάθετη στη δοκό, όπως φαίνεται στο σχήμα.
Γ2.
Βρείτε το έργο της δύναμης
F
κατά την περιστροφή του συστήματος μέχρι
την οριζόντια θέση της. (Μονάδες 6)
Γ3.
Βρείτε την γωνιακή ταχύτητα του συστήματος δοκού- σφαίρας στην
οριζόντια θέση. (Μονάδες 6)
Επαναφέρουμε το σύστημα δοκού-σφαίρας στην αρχική κατακόρυφη θέση
του. Ασκούμε στο άκρο
Α
δύναμη, σταθερού μέτρου
F 30 3 N
, που είναι
συνεχώς κάθετη στη δοκό.
Γ4.
Βρείτε τη γωνία που σχηματίζει η δοκός με την κατακόρυφο τη στιγμή που
η κινητική της ενέργεια γίνεται μέγιστη. (Μονάδες 7)
Δίνονται:
2
g 10m/s
, ροπή αδράνειας ομογενούς δοκού μάζας
Μ
και μήκους
ℓ, ως προς άξονα που διέρχεται από το κέντρο μάζας της και είναι κάθετος σε
αυτήν
2
cm
1
I
M
12
,
ημ60 συν30 3 / 2
,
ημ30 συν60 1 / 2
.
Απάντηση:
Γ1.
Με εφαρμογή του θεωρήματος Steiner η ροπή αδράνειας της δοκού
δίνεται:
A
F
m
O
ΘΕΜΑ Γ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2012









