7
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
και για
h 0
¹
,
F(x h) F(x) f(x h) f(x) g(x h) g(x)
h
h
h
+ -
+ -
+ -
=
+
.
Άρα
:
h 0
h 0
h 0
F(x h) F(x)
f(x h) f(x)
g(x h) g(x)
lim
lim
lim
f (x) g (x).
h
h
h
®
®
®
+ -
+ -
+ -
¢
¢
=
+
= +
Δηλαδή:
( ) ( ) ( )
F' x f ' x g' x
= +
Σχολικό βιβλίο, Σελ.
31.
Α.β)
Είναι:
·
( )
( )
c f x ' c f ' x
é ×
ù = ×
ë
û
·
( ) ( )
( ) ( ) ( ) ( )
f x g x ' f ' x g x f x g' x
é ×
ù =
×
+ ×
ë
û
·
( )
( )
( ) ( ) ( ) ( )
( )
2
'
f x
f ' x g x f x g' x
g x
g x
é
ù
×
- ×
=
ê
ú
ê
ú
ë
û
, με
( )
g x 0
¹
.
Σχολικό βιβλίο, Σελ.
31.
Β. α)
α
«
5,
β
«
1,
γ
«
7,
δ
«
2.
Β. β)
Για
x 0
¹
έχουμε:
( )
( )
( )
x
x
x
x
2
2
e x e x ' e x e
f ' x
x
x
× - ×
× -
=
=
, επομένως σωστό
είναι το Δ.
Α
.
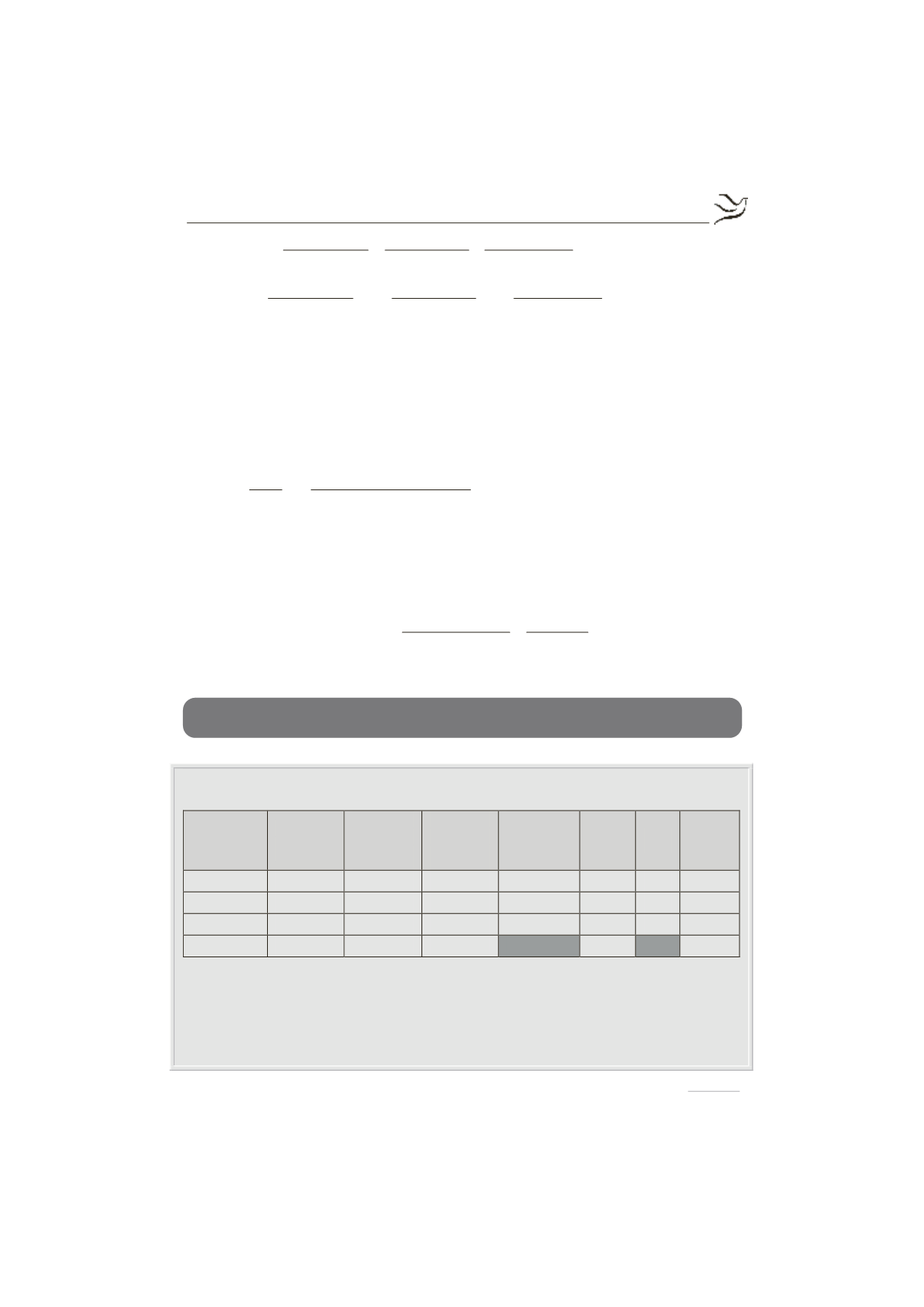
Να γράψετε στο τετράδιό σας τον πίνακα των τιμών της μεταβλητής Χ
σωστά συμπληρωμένο
.
Τιμές
μεταβλητής
i
x
Συχνότητα
i
ν
Σχετική
συχνότητα
i
f
Σχετική
Συχνότητα
i
f %
Αθροιστική
Συχνότητα
i
N
i
i
x
ν
×
2
i
x
2
i
i
x
ν
×
1
10
10
1
10
2
35
4
3
9
ΣΥΝΟΛΟ
ν 50
=
1
100
(Μονάδες 16
)
Β.
Να υπολογίσετε τη μέση τιμή και τη διάμεσο.
(Μονάδες
4)
Γ.
Να δείξετε ότι η διακύμανση είναι:
2
s 0,49
=
.
(Μονάδες 5)
ΘΕΜΑ Β
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2000









