341
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Θέμα 98
Αν
( )
(
)
(
)
x
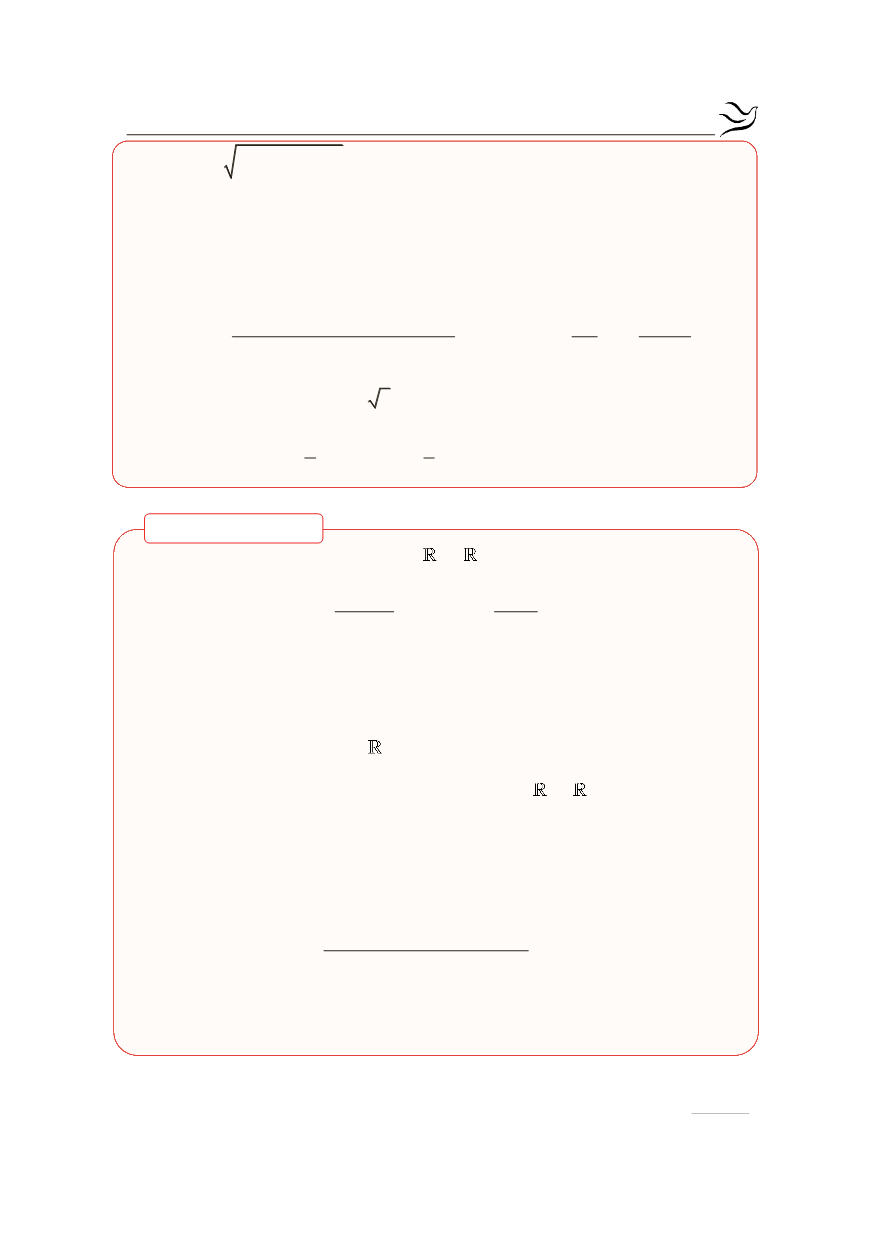
f x 1 e 1 1 x
= - - -
,
[ ]
x 0,1
Î
B.
Να δείξετε ότι η
f
έχει μόνο δύο μέγιστα και ότι υπάρχει μοναδικό
( )
0
x 0,1
Î
στο οποίο η
f
παρουσιάζει ελάχιστο.
Γ.
Να υπολογίσετε, εφόσον υπάρχουν, τα παρακάτω όρια
Γα
.
( ) ( )
(
)
(
)
0
0
x x
0
0
ημx ημx
lim
f x f x
συνx συνx
®
-
-
-
Γβ
.
x
x
x
x
lnx
3 5
lim f
ημ
x
7 1
®+¥
é
ù +
æ ö ×
ê
ú
ç ÷
+
è ø
ë
û
Δ.
Να αποδείξετε ότι
( )
f x 1 x
³ -
, για κάθε
[ ]
x 0,1
Î
.
Ε.
Να αποδείξετε ότι
( )
1
0
1
1
g x dx
6
2
- <
<
ò
.
Δίνεται η πολυωνυμική συνάρτηση
f :
®
για την οποία ισχύουν:
( )
x 1
f x 1
lim 2
x 1
®
-
=
-
και
( )
2
x
f x
lim 1
x 1
®+¥
=
+
και
Α.
Να δείξετε ότι
( )
f 1 1
=
και
( )
f 1 2
¢
=
.
Β.
Να δείξετε ότι
( )
2
f x x
=
,
x
Î
.
Γ.
Δίνεται επιπλέον η παραγωγίσιμη συνάρτηση
g :
®
η οποία έχει το ίδιο
ελάχιστο με την
f
στην μοναδική θέση
x
α
=
,
α 0
>
.
Γα.
Να δείξετε ότι οι γραφικές παραστάσεις των συναρτήσεων
f
και
g
έχουν
τουλάχιστον ένα κοινό σημείο
(
)
0 0
Μ x ,y
με
( )
0
x 0,
α
Î
.
Γβ.
Αν ισχύει ότι
( )
(
)
( )
(
)
( )
(
)
0
0
0
h 0
g g x h g g x h
lim
g
ημg x
2h
®
+ -
-
¢=
με
( )
0
x 0,
α
Î
τότε να δείξετε ότι η συνάρτηση
g
¢
δεν είναι αντιστρέψιμη.









