Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης
284
Δύο ράβδοι είναι συνδεδεμένες στο άκρο τους Α και σχηματίζουν σταθερή
γωνία 60
ο
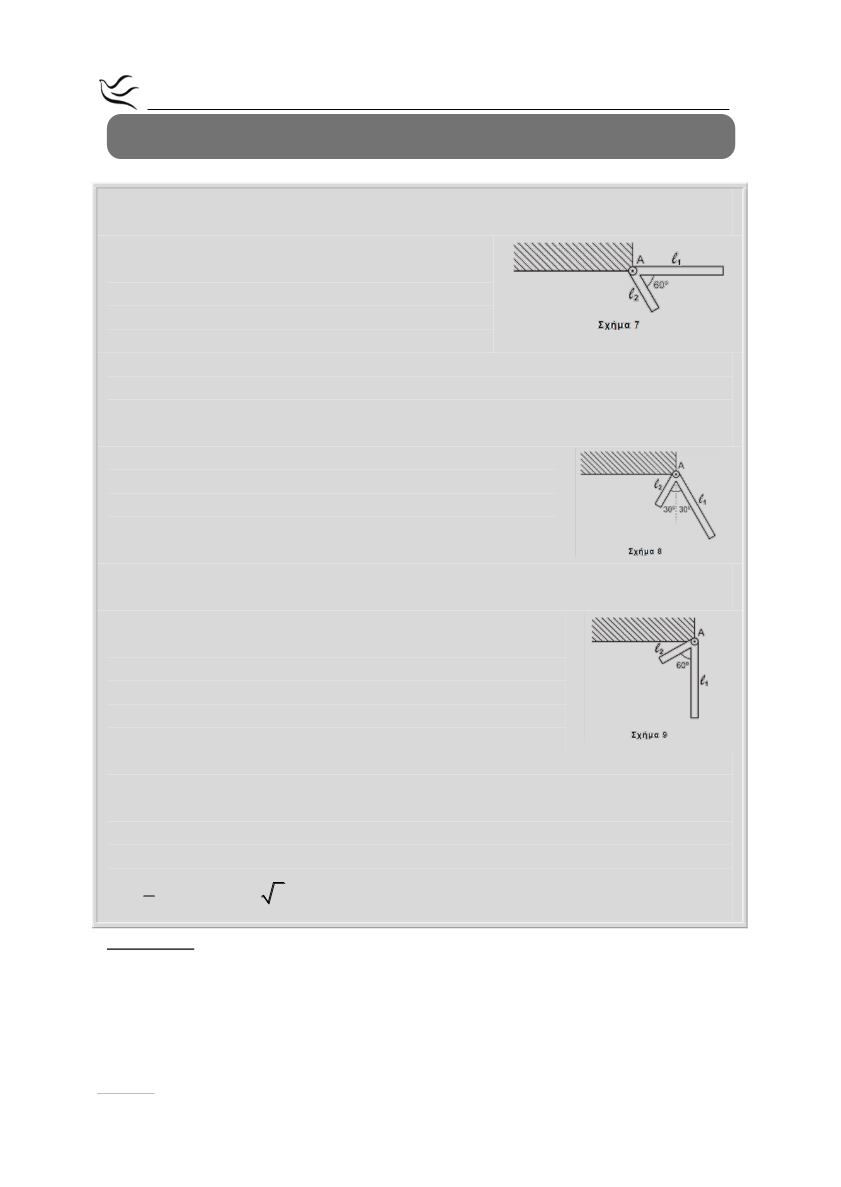
μεταξύ τους, όπως φαίνεται στο Σχήμα 7. Οι ράβδοι είναι
διαφορετικές μεταξύ τους, αλλά κάθε μία είναι
ομογενής. Το σύστημα των δύο ράβδων μπορεί
να περιστρέφεται γύρω από άρθρωση, που είναι
στερεωμένη σε τοίχο, στο άκρο Α, χωρίς τριβές.
Το σύστημα αφήνεται να περιστραφεί υπό την
επίδραση της βαρύτητας από τη θέση του Σχήματος 7, όπου η ράβδος ℓ
1
είναι
οριζόντια, με αρχική ταχύτητα μηδέν.
Δίνεται ότι τα μήκη των δύο ράβδων είναι ℓ
1
= 4m και ℓ
2
= 2m, ενώ η μάζα της
ράβδου ℓ
2
είναι m
2
= 10kg.
Γ1
. Να υπολογίσετε τη μάζα m
1
της ράβδου μήκους ℓ
1
,
εάν το σύστημα αποκτά τη μέγιστη γωνιακή ταχύτητα τη
χρονική στιγμή που οι δύο ράβδοι σχηματίζουν ίσες
γωνίες με την κατακόρυφο, όπως φαίνεται στο Σχήμα 8.
(Μονάδες 5)
Γ2.
Να υπολογίσετε τη μάζα m
1
της ράβδου μήκους ℓ
1
, εάν το σύστημα
σταματά στιγμιαία, όταν η ράβδος μήκους ℓ
1
φτάνει στην κατακόρυφη θέση
που φαίνεται στο Σχήμα 9.
(Μονάδες 7)
Γ3.
Να υπολογίσετε τη γωνιακή επιτάχυνση του
συστήματος των δύο ράβδων του ερωτήματος Γ2 στη
θέση που απεικονίζεται στο Σχήμα 9.
(Μονάδες 7)
Γ4.
Να υπολογίσετε τον ρυθμό μεταβολής της στροφορμής της ράβδου μήκους
ℓ
2
του ερωτήματος Γ2 στη θέση που απεικονίζεται στο Σχήμα 9.
(Μονάδες 6)
Δίνονται: η επιτάχυνση της βαρύτητας g=10m/s
2
, η ροπή αδρανείας ράβδου
μήκους ℓ και μάζας m που περιστρέφεται γύρω από το άκρο της Α
1 2
I = ml
Α 3
, και ότι
3
=1,7 (προσεγγιστικά).
Απάντηση:
Γ1.
Οι ροπές των βαρών των δύο ράβδων προκαλούν την περιστροφή περί το Α.
Αφού στη δοσμένη θέση επιτυγχάνεται η μέγιστη γωνιακή ταχύτητα σημαίνει
στο σημείο αυτό η συνολική ροπή μηδενίζεται και αμέσως μετά επιβραδύνεται.
Άρα στη θέση αυτή οι ροπές των δύο βαρών ως προς Α γίνονται ίσες (κατά
μέτρο). Έτσι:
Στ(Α) = 0 άρα w1 .(AO) - w2 .(BA) = 0
ΘΕΜΑ Γ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2015









