283
Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Β3
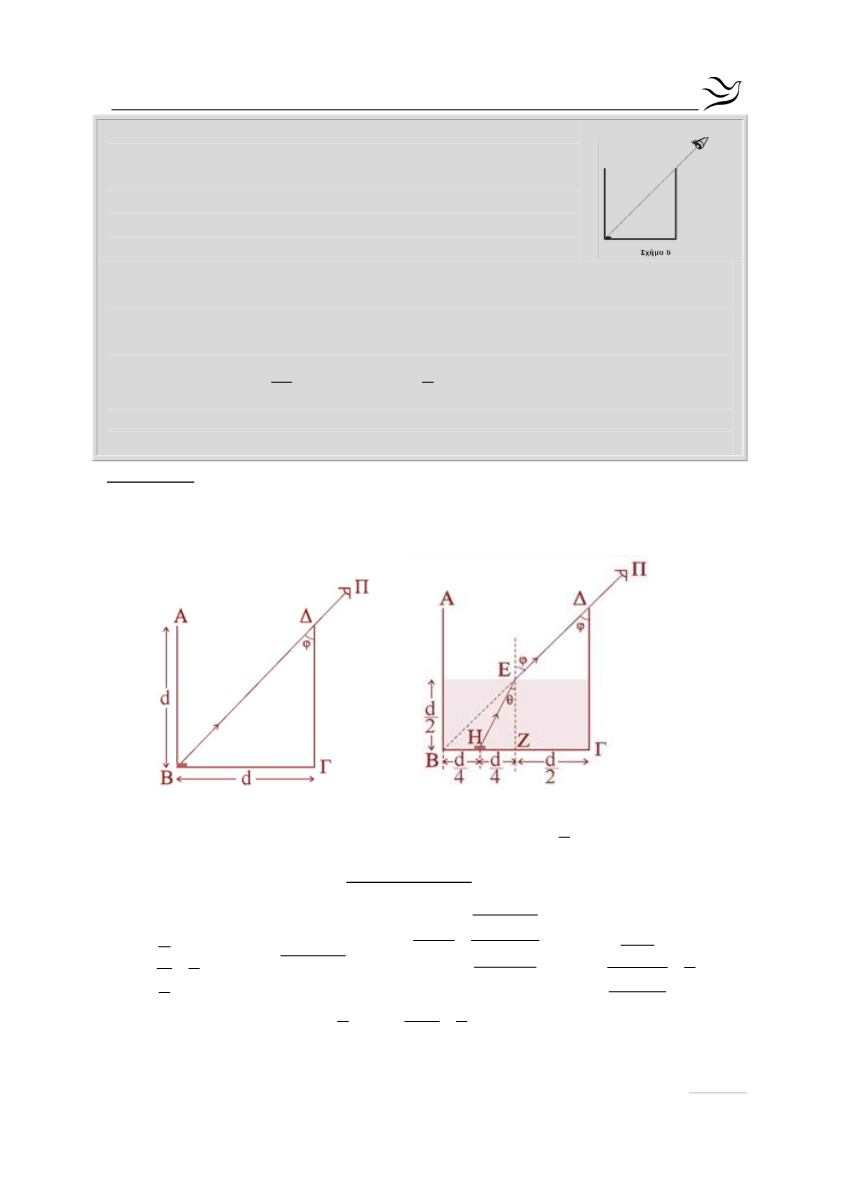
. Στο άκρο ενός δοχείου κυβικού σχήματος τοποθετείται
μικρό νόμισμα αμελητέων διαστάσεων. Ένας παρατηρητή
βλέπει “οριακά” το νόμισμα από τη θέση που βρίσκεται έξω
από το δοχείο, όπως απεικονίζεται στο Σχήμα 6. Στη
συνέχεια, γεμίζουμε το δοχείο με υγρό μέχρι το μέσο του,
οπότε ο παρατηρητής βλέπει πάλι “οριακά”, χωρίς να
αλλάξει τη θέση του ματιού του, το νόμισμα μετατοπισμένο κατά απόσταση
ίση με το 1/4 του μήκους της βάσης του δοχείου.
Το τετράγωνο του δείκτη διάθλασης του υγρού που προστέθηκε στο δοχείο
είναι
i)
n
2
=
13
8
ii)
n
2
=
5
2
iii)
n
2
=2
Να επιλέξετε τη σωστή απάντηση (Μονάδες 2)
Να δικαιολογήσετε την απάντησή σας (Μονάδες 7) (Μονάδες 9)
Απάντηση:
α. Σωστή απάντηση είναι η ii
β
.
Έστω d το μήκος των ακμών του κυβικού δοχείου και Π η σταθερή θέση του
παρατηρητή.
Από το σχήμα όταν το δοχείο είναι άδειο έχουμε:
d
εφφ= =1
d
Όταν γεμίσουμε το δοχείο και μετατοπίσουμε το κέρμα κατά d/4έχουμε:
d
1 4 εφθ = =
d 2
2
2
2
2
2
2
2
2
2
2
2
2
εφ φ
n.ημθ =1.ημφ
ημ φ 1+ εφ φ
1
n =
=
εφ φ
5
εφ θ
ημ φ =
ημ θ
1+1
n =
=
1+ εφ φ
1 / 4
1+ εφ θ
2
1+1 / 4
d
d / 4 1
εφφ = ,εφθ = =
d
d / 2 2









