Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης
162
Απάντηση:
Σωστή απάντηση είναι η (β)
1 2
2
f f
1
2
1
1
2
2
1
2
2
2
1
1
2
1
2π LC LC
f
f
LC
C C
1
f
f
LC
LC
2π LC
3.
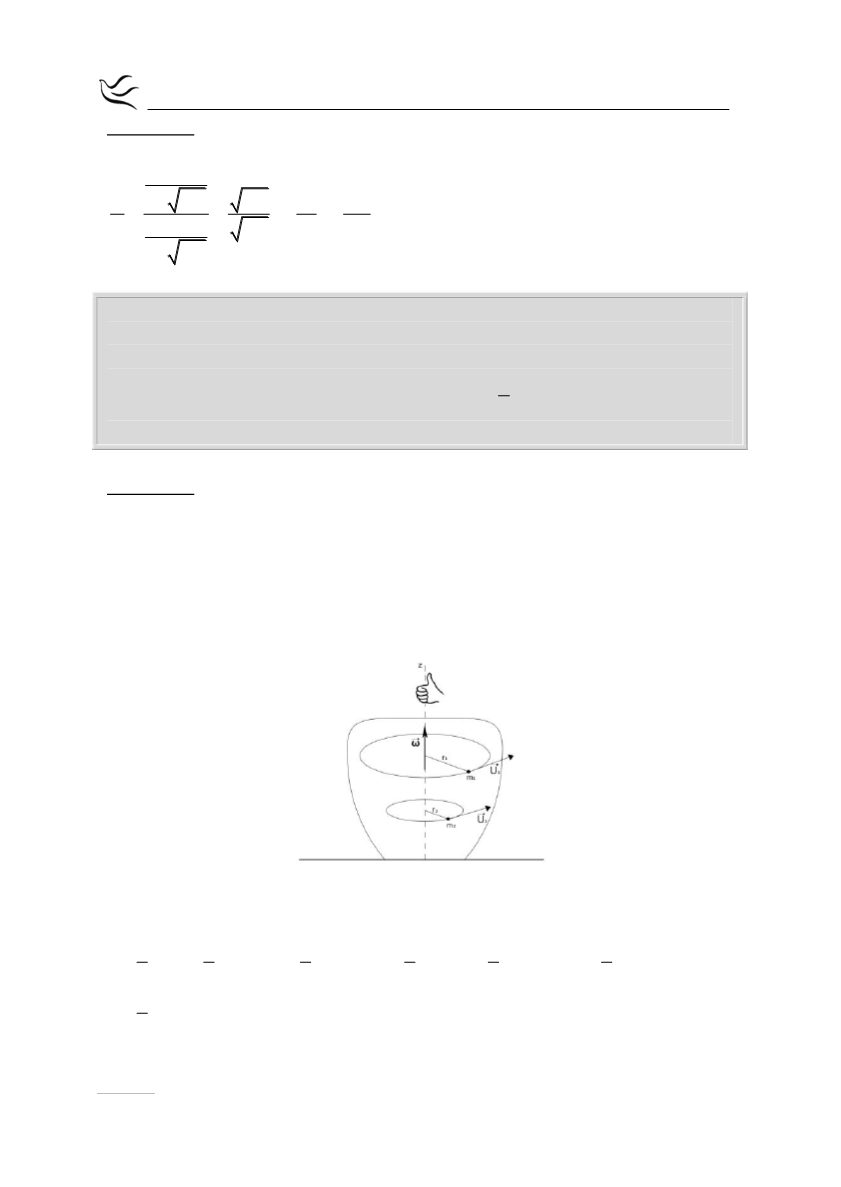
Στερεό σώμα περιστρέφεται γύρω από σταθερό άξονα με γωνιακή ταχύτητα
ω. Αν η ροπή αδράνειας του σώματος ως προς τον άξονα περιστροφής του
είναι Ι , να αποδείξετε ότι η κινητική ενέργεια του σώματος λόγω της
στροφικής του κίνησης δίνεται από τη σχέση
2
1
K Iω
2
. (Μονάδες
7)
Απάντηση:
Θεωρούμε ένα στερεό σώμα που στρέφεται με σταθερή γωνιακή ταχύτητα ω
γύρω από σταθερό άξονα z’z , όπως φαίνεται στο σχήμα. Χωρίζουμε το σώμα
σε στοιχειώδεις μάζες m
1 ,
m
2,. . . ,
m
n
, οι οποίες απέχουν από τον άξονα
περιστροφής αποστάσεις r
1
,r
2
,…,r
n
αντίστοιχα . fΤα μέτρα των γραμμικών τους
ταχυτήτων δίνονται από τις σχέσεις :
υ
1
=ωr
1
, υ
2
=ωr
2
, … , υ
n
=ωr
n
Κινητική ενέργεια του σώματος είναι ίση με το άθροισμα των κινητικών
ενεργειών των μαζών από τις οποίες αποτελείται :
2
2
2
2 2
2 2
2 2
1 1
2 2
n n
1 1
2 2
n n
2 2
2 2
2 2
2 2
2 2
2 2
1 1
2 2
n n
1 1
2 2
n n
1
1
1
1
1
1
K m υ m υ ...
m υ K m ω r
m ω r ...
m ω r
2
2
2
2
2
2
1
K m ω r m ω r ... m ω r όμως m ω r m ω r ... m ω r Ι
2









