11
Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
δ.
Η μέγιστη ταχύτητα με την οποία ταλαντώνεται ένα σημείο της χορδής έχει
μέτρο:
max
max
υ ωΑ υ 0,4πm/ s
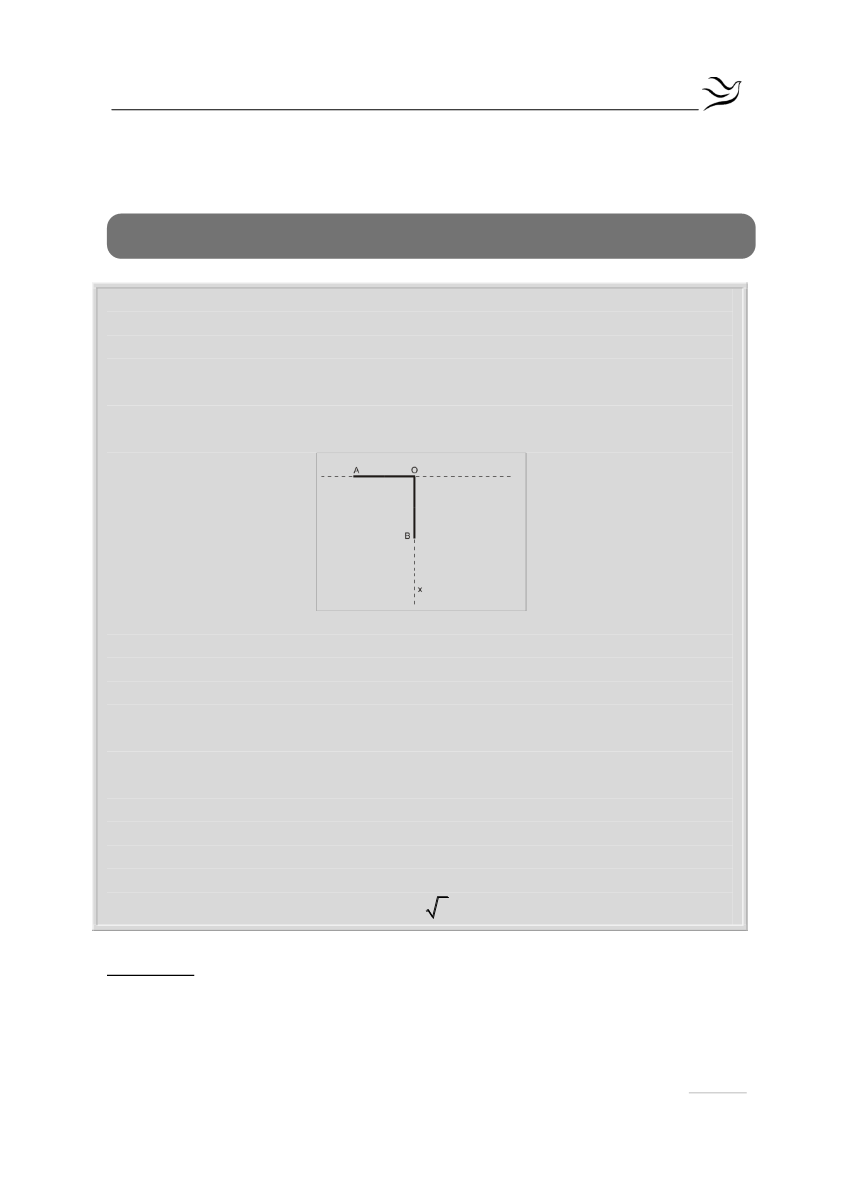
Δύο ίδιες, λεπτές, ισοπαχείς και ομογενείς ράβδοι ΟΑ και ΟΒ, που έχουν μάζα
Μ = 4 Κg και μήκος L = 1,5 m η καθεμία, συγκολλούνται στο ένα άκρο τους Ο,
ώστε να σχηματίζουν ορθή γωνία. Το σύστημα των δύο ράβδων μπορεί να
περιστρέφεται περί οριζόντιο άξονα, κάθετο στο επίπεδο ΑΟΒ, που διέρχεται
από την κορυφή Ο της ορθής γωνίας. Το σύστημα αρχικά συγκρατείται στη
θέση όπου η ράβδος ΟΑ είναι οριζόντια (όπως στο σχήμα). Η ροπή αδράνειας
της κάθε ράβδου ως προς το κέντρο μάζας της είναι I
cm
= (1/12) ML
2
.
Α.
Να υπολογίσετε τη ροπή αδράνειας της κάθε ράβδου ως προς τον άξονα
περιστροφής που διέρχεται από το Ο. (Μονάδες 6)
Β.
Από την αρχική του θέση το σύστημα των δύο ράβδων αφήνεται ελεύθερο
να περιστραφεί περί τον άξονα περιστροφής στο σημείο Ο, χωρίς τριβές. Να
υπολογίσετε το μέτρο της γωνιακής επιτάχυνσης του συστήματος των δύο
ράβδων τη στιγμή της εκκίνησης. (Μονάδες 6)
Γ.
Τη χρονική στιγμή κατά την οποία οι ράβδοι σχηματίζουν ίσες γωνίες με την
κατακόρυφο Οx, να υπολογίσετε:
α.
Το μέτρο της γωνιακής ταχύτητας του συστήματος των δύο ράβδων.
(Μονάδες 7)
β.
Το μέτρο της στροφορμής της κάθε ράβδου ως προς τον άξονα περιστροφής
που διέρχεται από το σημείο Ο. (Μονάδες 6)
Δίνονται:
2
g 10m/ s
, ημ45
ο
= συν45
ο
=
2 / 2
= 0,7.
Απάντηση:
A.
Η ροπή αδράνειας της μιας ράβδου ως προς τον άξονα περιστροφής που
διέρχεται από το άκρο Ο, θα υπολογιστεί με το θεώρημα των παραλλήλων
αξόνων (θεώρημα Steiner):
ΘΕΜΑ 4
ο
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2002









