Φυσική Γ' Λυκείου

10 / 290

9
Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Στο σύστημα δεν ασκείται εξωτερική ροπή, άρα η ολική στροφορμή του
συστήματος παραμένει σταθερή. Άρα θα ισχύει:
Ιαρχ  ω αρχ = Ιτελ  ωτελ
Επειδή ισχύει όμως Ι τελ < Ιαρχ θα ισχύει και ω τελ > ωαρχ , άρα ο δίσκος θα
περιστρέφεται πιο γρήγορα.
3. Σφαίρα μάζας m κινούμενη με ταχύτητα μέτρου υ1 συγκρούεται κεντρικά και
ελαστικά με ακίνητη σφαίρα ίσης μάζας. Να βρείτε τις σχέσεις που δίνουν τις
ταχύτητες των δύο σφαιρών, μετά την κρούση, με εφαρμογή των αρχών που
διέπουν την ελαστική κρούση. (Μονάδες 8)
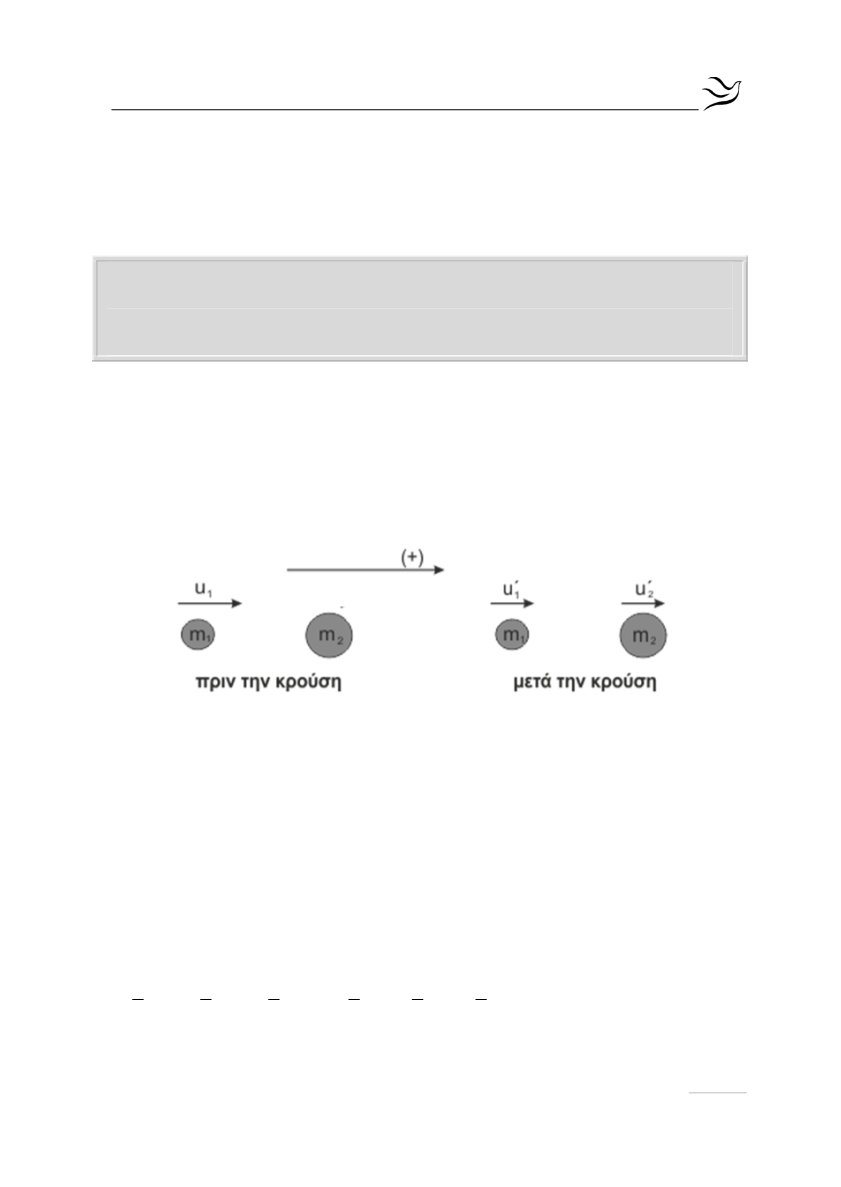
Έστω δύο σφαίρες με μάζες και τέτοιες ώστε  
1 2 m m m . Η ταχύτητα
της 1ης σφαίρας έχει μέτρο ενώ η δεύτερη σφαίρα είναι ακίνητη. Οι σφαίρες
συγκρούονται κεντρικά και ελαστικά με αποτέλεσμα μετά την κρούση οι
ταχύτητες τους να έχουν μέτρο και όπως φαίνεται στο σχήμα. Για να
υπολογίσουμε τις ταχύτητες των σφαιρών μετά την κρούση εργαζόμαστε ως
εξής:
Κατά τη διάρκεια της κρούσης των δύο σφαιρών το σύστημα τους θεωρείται
μονωμένο. Άρα ισχύει η ΑΔΟ:
   
 

ολ πριν ολ μετά p p
Η κρούση είναι κεντρική, άρα η παραπάνω διανυσματική έκφραση της ΑΔΟ
μεταπίπτει σε αλγεβρική:
 
       
1 1 1 1 2 2 1 1 2 1 1 2 m u m u' m u' mu mu' mu' u u' u' 1
Η κρούση είναι ελαστική άρα:
    
ολ αρχ ολ τελ K Κ
 
        2 2 2 2 2 2 2 2 2
1 1 1 1 2 2 1 1 2 1 1 2
1 1 1 1 1 1
m u m u' m u' mu mu' mu' u u' u' 2
2 2 2 2 2 2
Η εξίσωση (1) γράφεται:  
 
1 1 2 u u' u' 3