Φυσική - Χημεία Γ' Λυκείου

179 / 194

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – τυπολόγια Φυσικής- Χημείας Γ΄θετικών σπουδών
178
ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
Ένα σύστημα κάνει εξαναγκασμένη ταλάντωση όταν δρα πάνω του μία
εξωτερική περιοδική δύναμη (διεγέρτης). Στην εξαναγκασμένη ταλάντωση το
σύστημα έχει την συχνότητα f δ του διεγέρτη και όχι την ιδιοσυχνότητά του fo
δηλαδή την συχνότητα της ελεύθερης ταλάντωσης. διεγ ρτη f f
έ
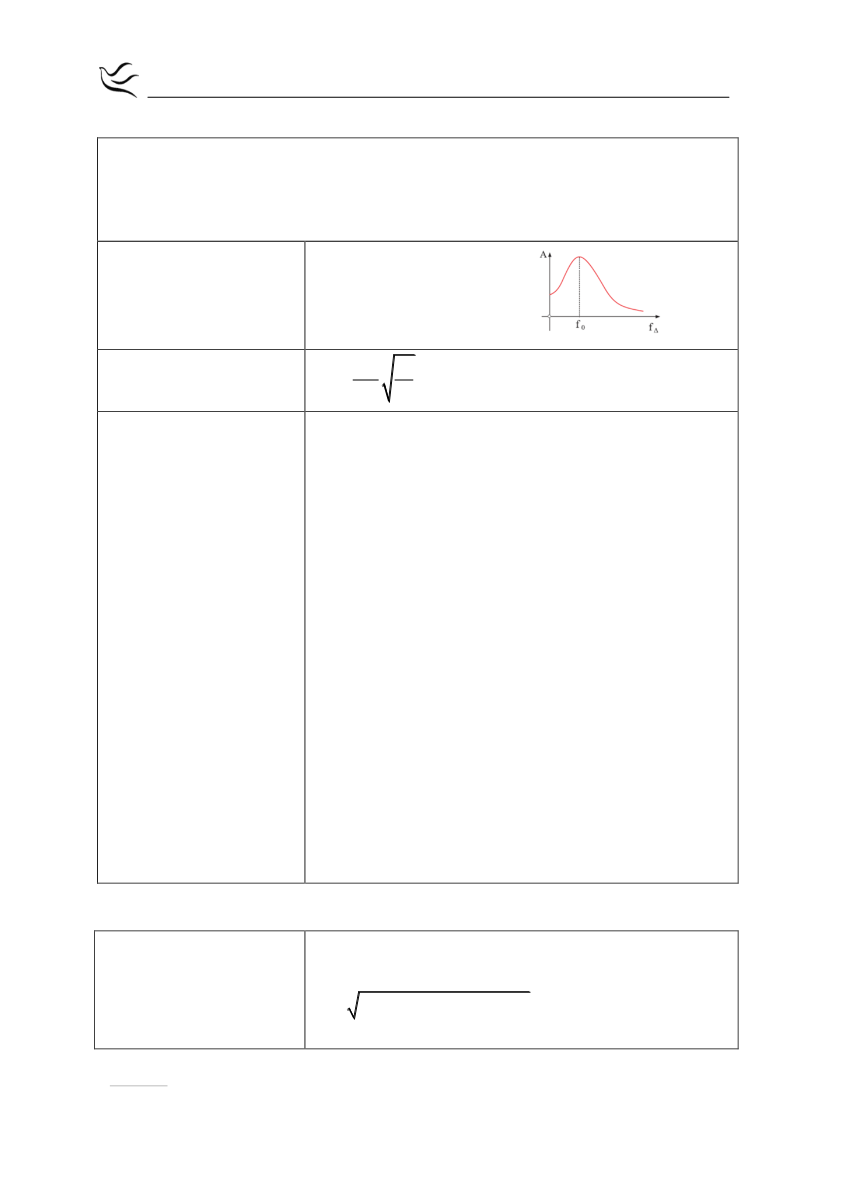
Καμπύλη συντονισμού διεγ ρτη
f f
0

έ
οπότε Α = μέγιστο
Ιδιοσυχνότητα
αρμονικού ταλαντωτή 0
1 D
f
2π m

Μεθοδολογία
Πάντα σχεδιάζουμε το διάγραμμα πλάτους – συχνότητας.
Μεταβάλλοντας την συχνότητα του διεγέρτη τότε:
 όταν πλησιάζουμε την συχνότητα συντονισμού (f0) το
πλάτος αυξάνεται και όταν απομακρυνόμαστε το
πλάτος μειώνεται .
 όταν υπάρχουν δυο συχνότητες που έχουμε ίδιο
πλάτος ,τότε η ιδιοσυχνότητα (f0) βρίσκεται μεταξύ
των δυο αυτών συχνοτήτων .
 πάντα η συχνότητα του συστήματος ισούται με αυτή
του διεγέρτη
 στην κατάσταση συντονισμού η συχνότητα του
διεγέρτη (fδ) ισούται με την ιδιοσυχνότητα (f0)
 στην κατάσταση συντονισμού το πλάτος του διεγέρτη
ΔΕΝ είναι ίδιο με αυτό του συστήματος
 στην κατάσταση συντονισμού η ενέργεια του
διεγέρτη ΔΕΝ ισούται με αυτή του συστήματος
 ΑΠΛΑ στον συντονισμό η (fδ) = (f0) ,
το πλάτος του συστήματος είναι μέγιστο ≠ από το πλάτος
του διεγέρτη
το σύστημα απορροφά το μεγαλύτερο δυνατό ποσοστό
της ενεργείας του διεγέρτη , άρα Εσυστημ ≠ Ε διεγερτη
ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ
Σύνθεση δύο Α.Α.Τ. της
ίδιας συχνότητας, που
γίνονται γύρω από το
ίδιο σημείο στην ίδια
διεύθυνση.
Αρχή της επαλληλίας : x = x1+x2
1 1 x A ημωt και  
2 2 x A ημ ωt φ 
2 2
1 2 1 2 Α Α Α 2Α Α συνφ  