133
Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
άρθρωση. (Μονάδες 4)
Μικρή ομογενής σφαίρα, μάζας m = 0,4 kg και ακτίνας
1
r
m
70
κυλίεται χωρίς
ολίσθηση, έχοντας εκτοξευθεί κατά μήκος της ράβδου από το σημείο Κ προς το
άκρο Γ.
Δ2.
Να βρεθεί η γωνιακή επιτάχυνση της σφαίρας κατά την κίνησή της από
το Κ μέχρι το Γ. (Μονάδες 5)
Δ3.
Με δεδομένο ότι η σφαίρα φτάνει στο άκρο Γ, να βρείτε τη σχέση που
περιγράφει την τάση του νήματος σε συνάρτηση με την απόσταση του σημείου
επαφής της σφαίρας με τη ράβδο, από το σημείο Κ.
(Μονάδες 5)
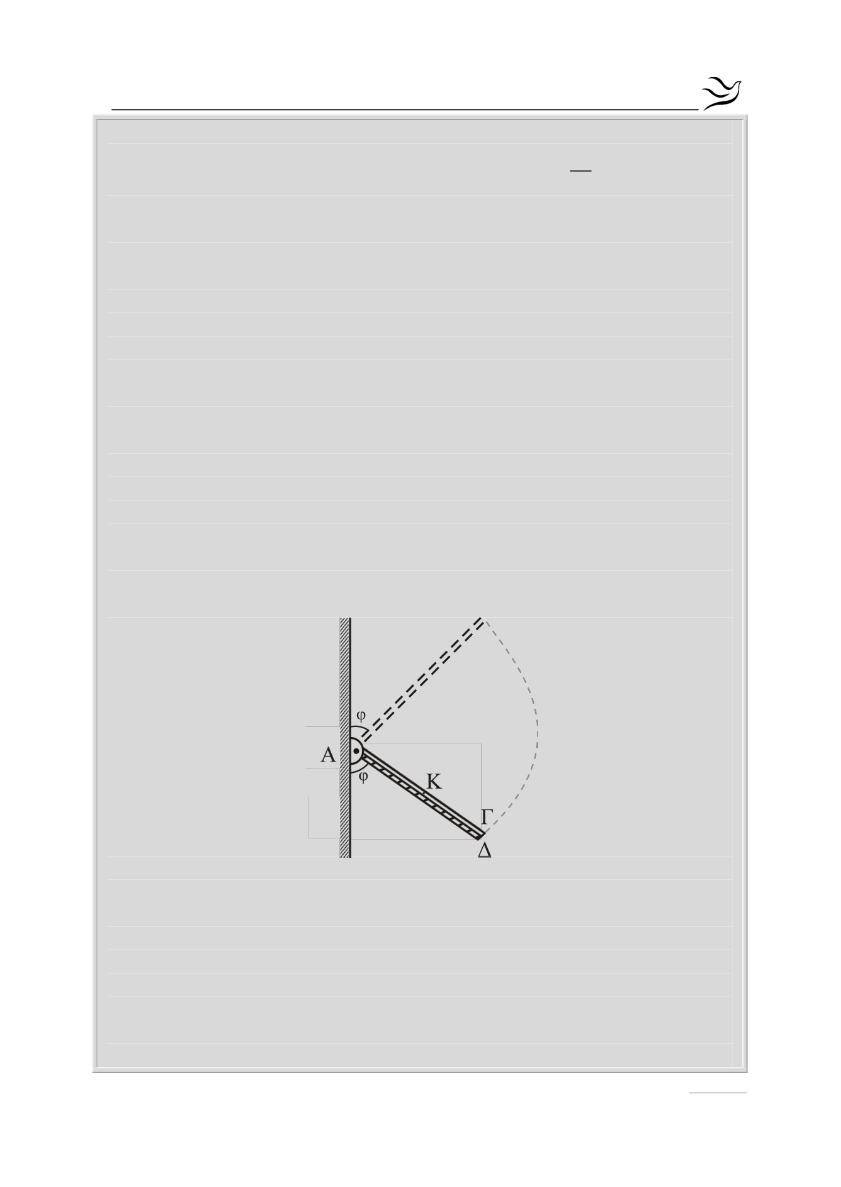
Αφού η σφαίρα έχει εγκαταλείψει τη ράβδο, κόβουμε το νήμα. Η ράβδος
στρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα, ο οποίος
διέρχεται από το άκρο της Α, χωρίς τριβές.
Δ4.
Να υπολογίσετε τον ρυθμό μεταβολής της κινητικής ενέργειας της
ράβδου στη θέση στην οποία η ράβδος σχηματίζει γωνία φ με την κατακόρυφο
που διέρχεται από το άκρο Α, όπως στο παρακάτω σχήμα.
(Μονάδες 6)
Δεύτερη λεπτή, άκαμπτη και ομογενής ράβδος ΑΔ, μήκους ℓ΄ = ℓ και μάζας
Μ΄=3Μ είναι αρθρωμένη και αυτή στο σημείο Α γύρω από τον ίδιο άξονα
περιστροφής με την ράβδο ΑΓ. Η ράβδος ΑΔ συγκρατείται ακίνητη, με
κατάλληλο μηχανισμό, σε θέση όπου σχηματίζει γωνία φ με τον κατακόρυφο
τοίχο όπως στο σχήμα. Οι δύο ράβδοι συγκρούονται και ταυτόχρονα ο
μηχανισμός ελευθερώνει τη ράβδο ΑΔ, χωρίς απώλεια ενέργειας. Οι ράβδοι
μετά την κρούση κινούνται σαν ένα σώμα, χωρίς τριβές. Ο χρόνος της κρούσης
θεωρείται αμελητέος.
Δ5.
Να υπολογίσετε το ποσοστό απώλειας της κινητικής ενέργειας του









