Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης
216
Στην επιφάνεια ενός ομογενούς κυλίνδρου μάζας Μ=40kg και ακτίνας R=0.2m,
έχουμε τυλίξει λεπτό σχοινί αμελητέας μάζας, το ελεύθερο άκρο του οποίου
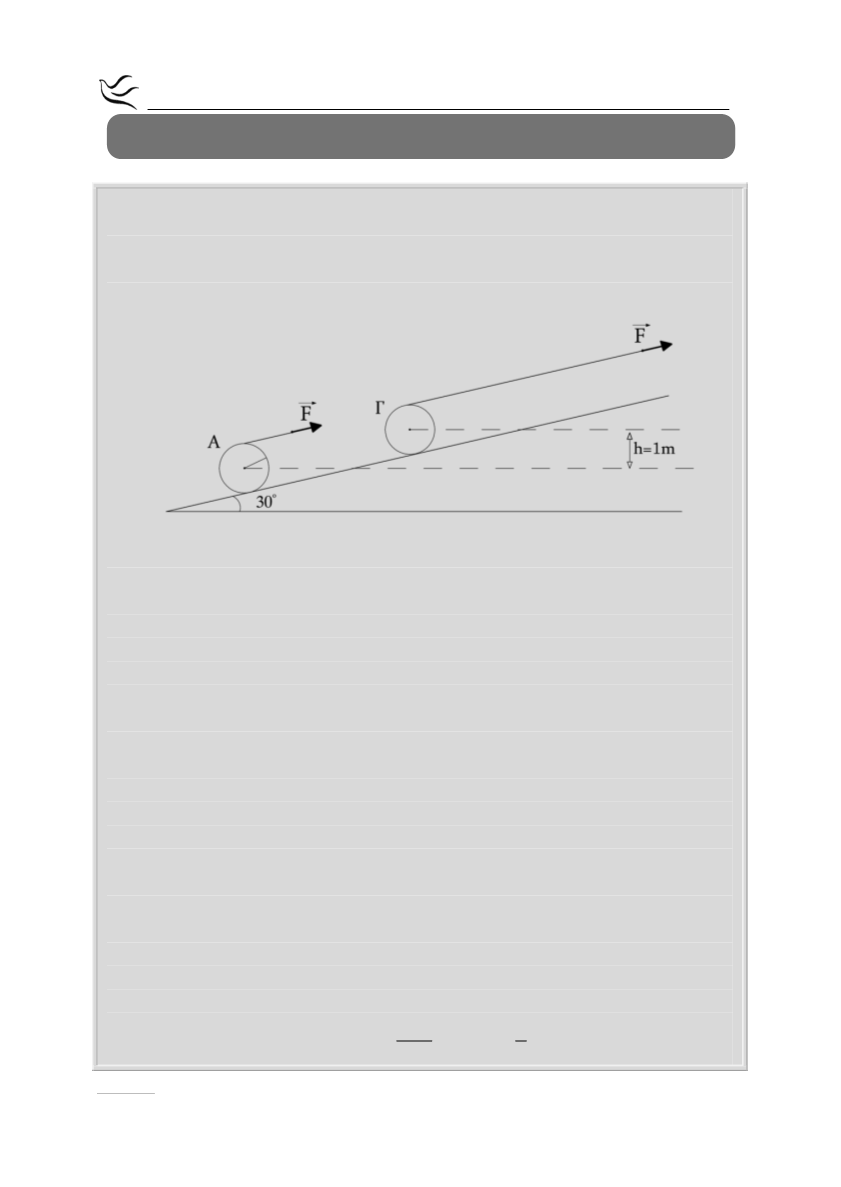
έλκεται με σταθερή δύναμη F παράλληλη προς την επιφάνεια κεκλιμένου
επιπέδου γωνίας κλίσεως 30
ο
, όπως φαίνεται στο σχήμα.
Το σχοινί ξετυλίγεται χωρίς ολίσθηση, περιστρέφοντας ταυτόχρονα τον
κύλινδρο. Ο κύλινδρος κυλίεται πάνω στην επιφάνεια του κεκλιμένου
επιπέδου χωρίς ολίσθηση.
α.
Να υπολογιστεί το μέτρο της δύναμη F, ώστε ο κύλινδρος να ανεβαίνει στο
κεκλιμένο επίπεδο με σταθερή ταχύτητα. (Μονάδες 5)
Αν αρχικά ο κύλινδρος είναι ακίνητος με το κέντρο μάζας του στη θέση Α και
στο ελεύθερο άκρο του σχοινιού ασκηθεί σταθερή δύναμη F=130N , όπως στο
σχήμα:
β.
Να υπολογιστεί η επιτάχυνση του κέντρου μάζας του κυλίνδρου.
(Μονάδες 6)
γ.
Να υπολογιστεί το μέτρο της στροφορμής του κυλίνδρου ως προς τον άξονα
περιστροφής του όταν το κέντρο μάζας του περνάει από τη θέση Γ του
σχήματος, η οποία βρίσκεται h=1m ψηλότερα από τη θέση Α. (Μονάδες 7)
δ.
Να υπολογιστεί το έργο της δύναμης F κατά τη μετακίνηση του κέντρου
μάζας του κυλίνδρου από τη θέση Α στη θέση Γ και να δείξετε ότι αυτό ισούται
με τη μεταβολή της μηχανικής ενέργειας του κυλίνδρου κατά τη μετακίνηση
αυτή.
(Μονάδες 7)
Δίνονται: επιτάχυνση βαρύτητας g=10m/s
2
, ροπή αδράνειας του κυλίνδρου ως
προς τον άξονα περιστροφής του
2
ο
MR
1
Ι
, ημ30
2
2
.
ΘΕΜΑ 4
Ο
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2009









