Εκδόσεις ΜΠΑΧΑΡΑΚΗ –
Φυσική Ομάδας Προσανατολισμού Θετικών Σπουδών
70
Δl
1
=2Δl
2
άρα Α
1
=2Α
2
2
2
2
2
2
2
1
2
1
2 2
1 1
2 2
1 1
2 2
1 2
2
1
2
1
1
2
2
2
2 4
8
8
2
2
k
k l
k l
k A k A k A k A k k
k
B2.
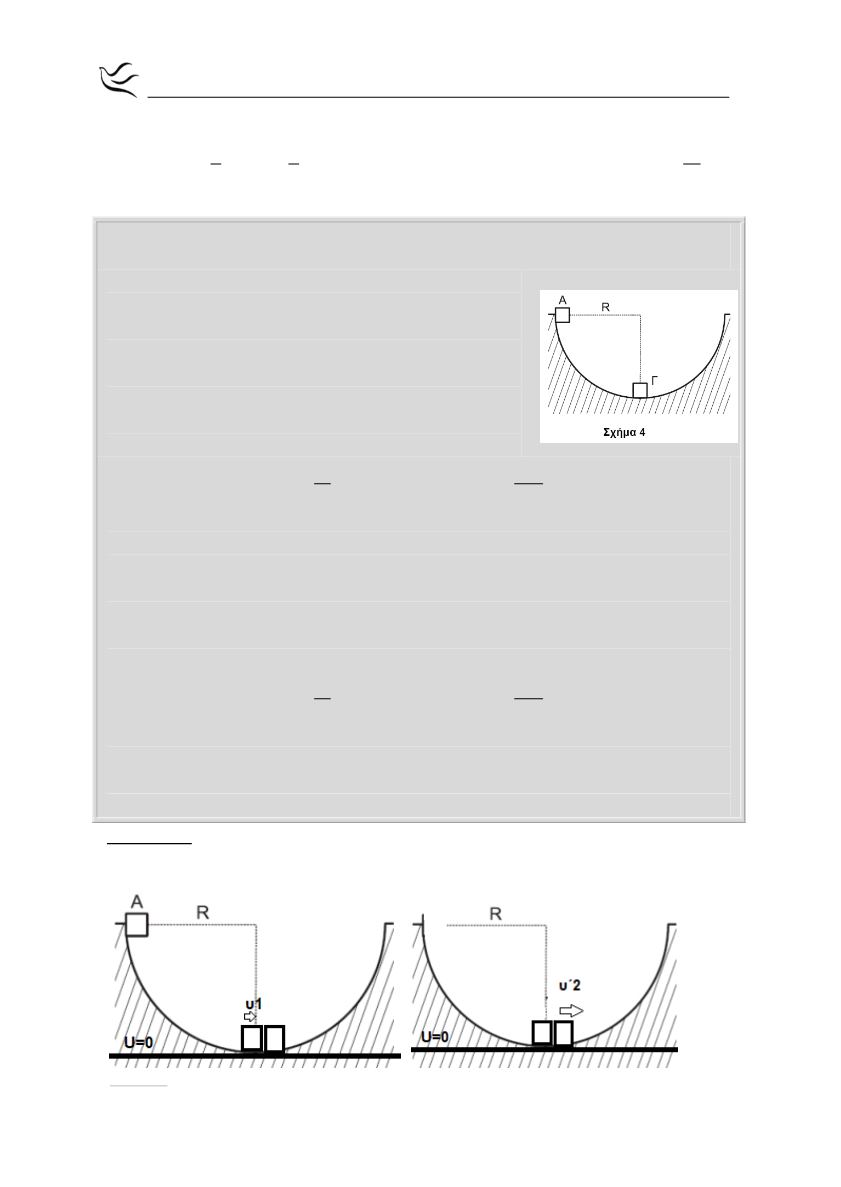
Από το εσωτερικό άκρο Α ενός ημισφαιρίου ακτίνας R (Σχήμα 4) αφήνεται
ελεύθερη μάζα m
1
αμελητέων διαστάσεων. Στο κατώτατο σημείο Γ του
ημισφαιρίου είναι ακίνητη μια πανομοιότυπη μάζα
m
2
(m
1
=m
2
=m) αμελητέων διαστάσεων. Οι τριβές
θεωρούνται αμελητέες.
B2.Α.
Η μάζα m
1
συγκρούεται με τη μάζα m
2
κεντρικά και ελαστικά. Μετά την κρούση η μάζα m
2
θα ανέλθει σε ύψος Η ως προς το κατώτατο σημείο
του ημισφαιρίου ίσο με
α)
R
4
β) R γ)
3R
2
Να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση.
Μονάδες 1
Να αιτιολογήσετε την επιλογή σας.
Μονάδες 3
B2.Β.
Η μάζα m
1
συγκρούεται με τη μάζα m
2
μετωπικά και πλαστικά. Μετά την
κρούση το συσσωμάτωμα θα ανέλθει σε ύψος h ως προς το κατώτατο σημείο
του ημισφαιρίου ίσο με
α)
R
4
β) R γ)
3R
2
Να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση.
Μονάδες 1
Να αιτιολογήσετε την επιλογή σας.
Μονάδες 3
Απάντηση:
B2.A Σωστό το (β)









