Εκδόσεις ΜΠΑΧΑΡΑΚΗ –
Φυσική Ομάδας Προσανατολισμού Θετικών Σπουδών
10
2
2
2
2
A
1
1
1
1
P
P
(1)
2
2
2
2
Εξίσωση συνέχειας: Π
1
= Π
2
Α
Α
∙υ
Α
= Α
Β
∙υ
Β
2Α
Β
∙υ
Α
= Α
Β
∙υ
Β
1
2 (2)
και
(2)
2
2
1
1
4 4 (3)
2
2
από (1), (3)
Ρ
A
Ρ
B
= 3 Λ
άρα σωστό το (ii).
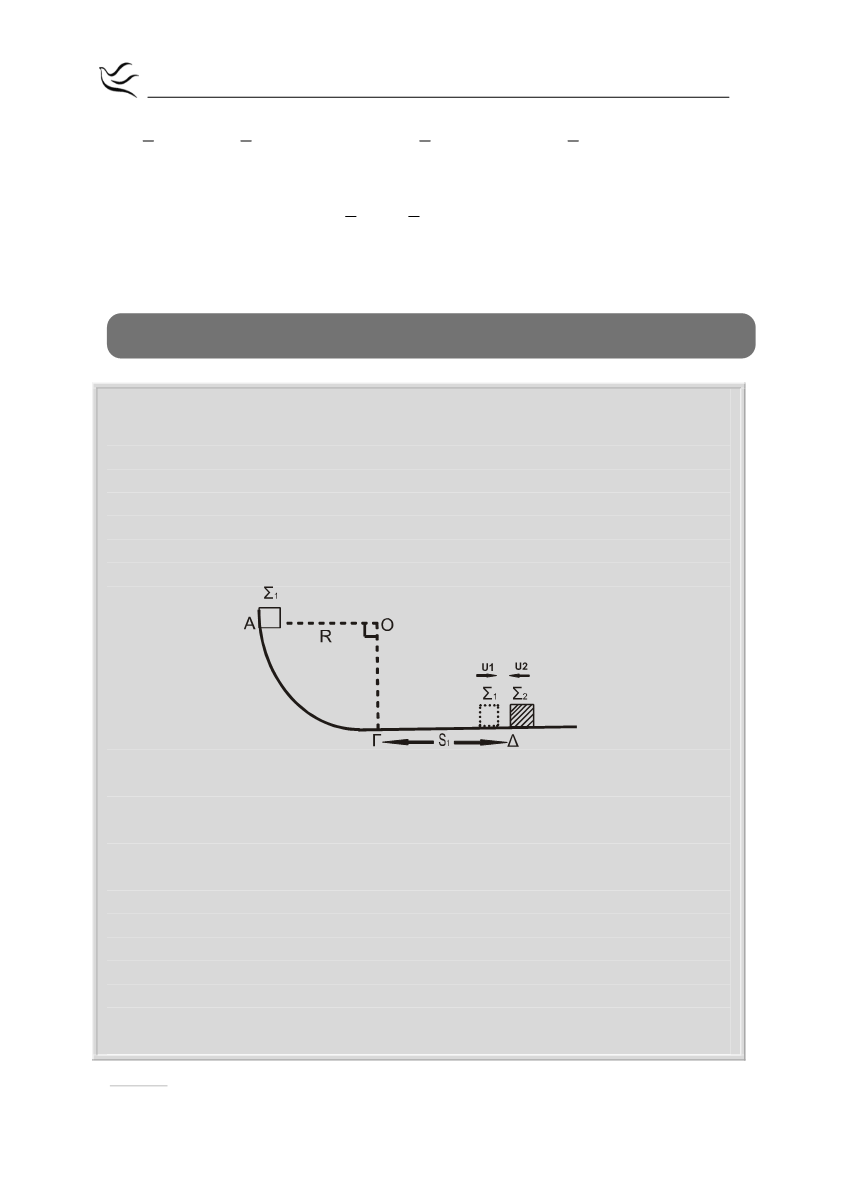
Σώμα Σ1 μάζας m
1
βρίσκεται στο σημείο Α λείου κατακόρυφου τεταρτοκυκλίου
( )
. Η ακτίνα ΟΑ είναι οριζόντια και ίση με R=5m. Το σώμα αφήνεται να
ολισθήσει κατά μήκος του τεταρτοκυκλίου. Φθάνοντας στο σημείο Γ του
τεταρτοκυκλίου, το σώμα συνεχίζει την κίνησή του σε οριζόντιο επίπεδο με το
οποίο εμφανίζει συντελεστή τριβής μ=0,5. Αφού διανύσει διάστημα S
1
=3,6m,
συγκρούεται κεντρικά και ελαστικά στο σημείο Δ με σώμα Σ2 μάζας m
2
=3m
1
,
το οποίο τη στιγμή της κρούσης κινείται αντίθετα ως προς το Σ1, με ταχύτητα
μέτρου u
2
= 4 m/s, όπως φαίνεται στο σχήμα 4.
Σχήμα 4
Γ1.
Να υπολογίσετε το μέτρο της ταχύτητας του σώματος Σ1 στο σημείο Γ,
όπου η ακτίνα ΟΓ είναι κατακόρυφη.
Μονάδες 5
Γ2.
Να υπολογίσετε τα μέτρα των ταχυτήτων των σωμάτων Σ1 και Σ2
αμέσως μετά την κρούση.
Μονάδες 8
Γ3.
Δίνεται η μάζα του σώματος Σ2, m
2
=3kg. Να υπολογίσετε το μέτρο της
μεταβολής της ορμής του σώματος Σ2 κατά την κρούση (μονάδες 3) και να
προσδιορίσετε την κατεύθυνσή της (μονάδες 2).
Μονάδες 5
Γ4.
Να υπολογίσετε το ποσοστό της μεταβολής της κινητικής ενέργειας
του σώματος Σ1 κατά την κρούση.
ΘΕΜΑ Γ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2016









