235
Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
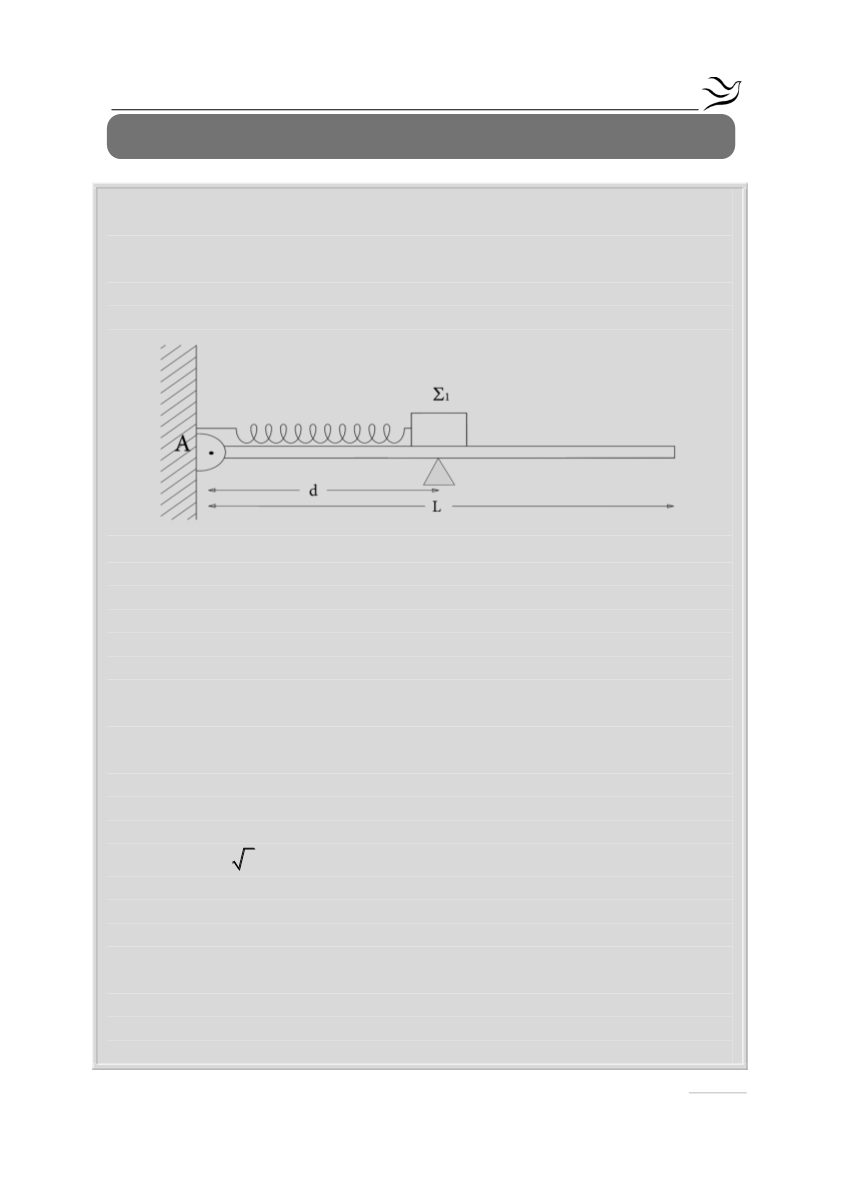
Λεία οριζόντια σανίδα μήκους L=3m και μάζας M=0,4 Kg αρθρώνεται στο άκρο
της Α σε κατακόρυφο τοίχο. Σε απόσταση d=1m από τον τοίχο, η σανίδα
στηρίζεται ώστε να διατηρείται οριζόντια. Ιδανικό αβαρές ελατήριο σταθεράς
Κ=100 Ν/m συνδέεται με το ένα άκρο του στον τοίχο και το άλλο σε σώμα Σ
1
μάζας m
1
=1kg. Το ελατήριο βρίσκεται στο φυσικό του μήκος, ο άξονάς του
είναι οριζόντιος και διέρχεται από το κέντρο μάζας του σώματος Σ
1
.
Το κέντρο μάζας του σώματος
1
Σ
βρίσκεται σε απόσταση d από τον τοίχο. Στη
συνέχεια ασκούμε στο σώμα Σ
1
σταθερή οριζόντια δύναμη μέτρου F=40N με
κατεύθυνση προς το άλλο άκρο Γ της σανίδας. Όταν το σώμα Σ
1
διανύσει
απόσταση s=5cm, η δύναμη παύει να ασκείται στο σώμα και στη συνέχεια το
σώμα εκτελεί απλά αρμονική ταλάντωση.
Δ1.
Να υπολογίσετε το πλάτος της απλής αρμονικής ταλάντωσης που θα
εκτελέσει το σώμα Σ
1
. (Μονάδες 5)
Δ2.
Να εκφράσετε το μέτρο της δύναμης F
A
που δέχεται τη σανίδα από τον
τοίχο σε συνάρτηση με την απομάκρυνση του σώματος Σ
1
και να σχεδιάσετε
την αντίστοιχη γραφική παράσταση. Για το σχεδιασμό της γραφικής
παράστασης να χρησιμοποιηθεί χαρτί μιλιμετρέ.
(Μονάδες 7)
Κατά μήκος της σανίδας από το άκρο Γ κινείται σώμα Σ
2
μάζας m
2
= 1Kg με
ταχύτητα
2
υ 2 3
m/s. Τα δύο σώματα συγκρούονται κεντρικά και ελαστικά,
όταν η απομάκρυνση του σώματος Σ
1
είναι x
1
, όπου x
1
≥0. Το σώμα Σ
1
μετά την
κρούση ταλαντώνεται με το μέγιστο δυνατό πλάτος.
Δ3.
Να βρείτε την απομάκρυνση x
1
. (Μονάδες 6)
Δ4.
Να βρείτε μετά από πόσο χρονικό διάστημα από τη στιγμή της κρούσης τα
δύο σώματα θα συγκρουστούν για δεύτερη φορά. (Μονάδες 7)
Θεωρούμε θετική τη φορά της απομάκρυνσης προς το Γ. Τριβές στην άρθρωση
και στο υποστήριγμα δεν υπάρχουν.
Δίνεται: επιτάχυνση βαρύτητας g=10m/s
2
.
ΘΕΜΑ Δ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2011









