193
Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
δ.
max
Τ
t x
π
13,5
π
4
u u συν2π
u συν2π
u m/ s
T λ
5
Τ 6
5
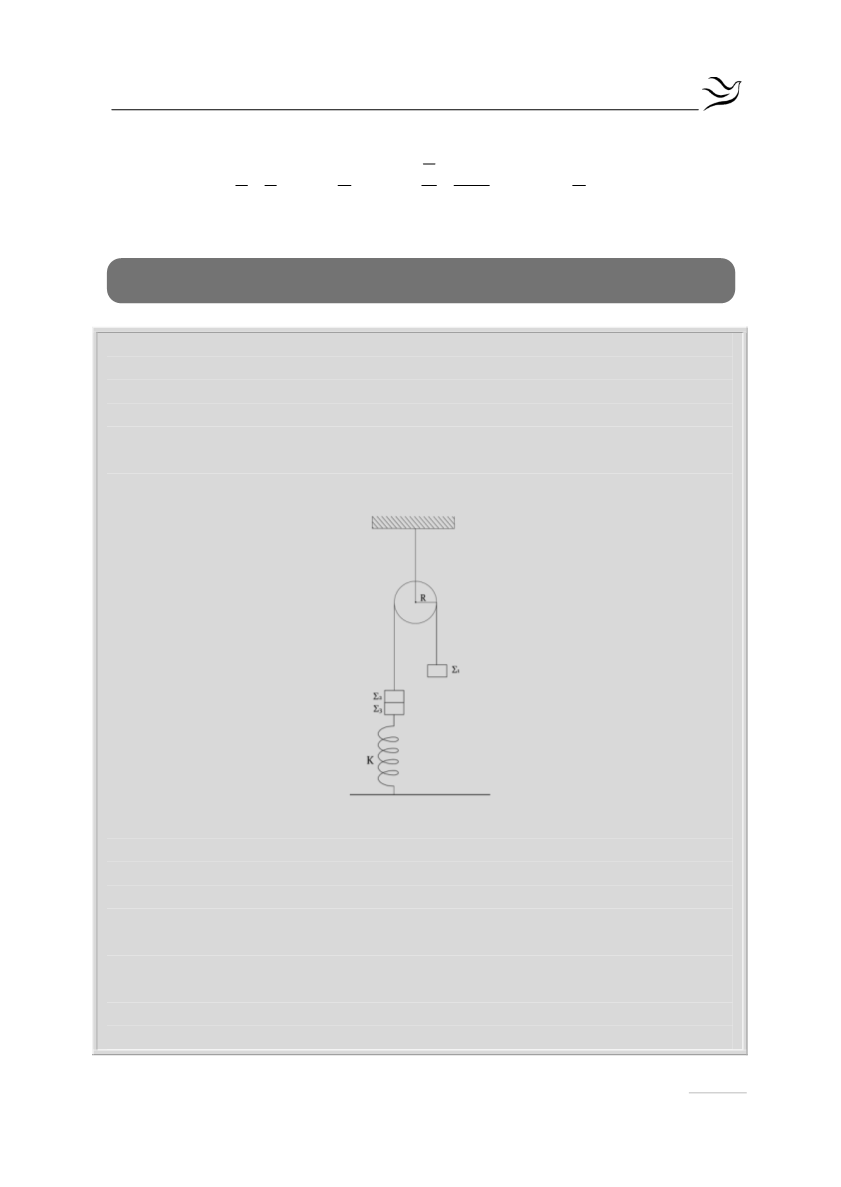
Τροχαλία μάζας Μ= 6kg και ακτίνας R=0,25m μπορεί να περιστρέφεται χωρίς
τριβές γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο της. Γύρω από
την τροχαλία υπάρχει αβαρές και μη εκτατό νήμα. Στα άκρα του νήματος
υπάρχουν σε κατακόρυφη θέση τα σώματα Σ
1
και Σ
2
με μάζες m
1
=4kg και
m
2
=1kg αντίστοιχα. Το σώμα Σ
2
είναι κολλημένο με σώμα Σ
3
μάζας m
3
=1kg, το
οποίο συγκρατείται από κατακόρυφο ελατήριο σταθεράς Κ=100Ν/m. Το
σύστημα αρχικά ισορροπεί όπως φαίνεται στο σχήμα.
Κάπoια χρονική στιγμή, την οποία θεωρούμε ως χρονική στιγμή 0 (t
0
=0), τα
σώματα Σ
2
και Σ
3
αποκολλώνται και το Σ
3
εκτελεί απλή αρμονική ταλάντωση
κατά τη διεύθυνση της κατακορύφου.
α.
Να υπολογιστεί το πλάτος της ταλάντωσης του σώματος Σ
3
. (Μονάδες 6)
β.
Να γραφεί η εξίσωση της απομάκρυνσης του σώματος Σ
3
σε συνάρτηση με
το χρόνο, θεωρώντας ως θετική φορά, τη φορά προς τα επάνω. (Μονάδες 6)
γ.
Να υπολογιστεί η γωνιακή επιτάχυνση της τροχαλίας μετά την αποκόλληση
των σωμάτων Σ
2
και Σ
3
. (Μονάδες 6)
δ.
Να υπολογιστεί ο ρυθμός μεταβολής της κινητικής ενέργειας της τροχαλίας
τη χρονική στιγμή t=0,1 s. (Μονάδες 7)
ΘΕΜΑ 4
Ο
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2006









