63
Φυσική Ομάδας Προσανατολισμού Θετικών Σπουδών –
Εκδόσεις ΜΠΑΧΑΡΑΚΗ
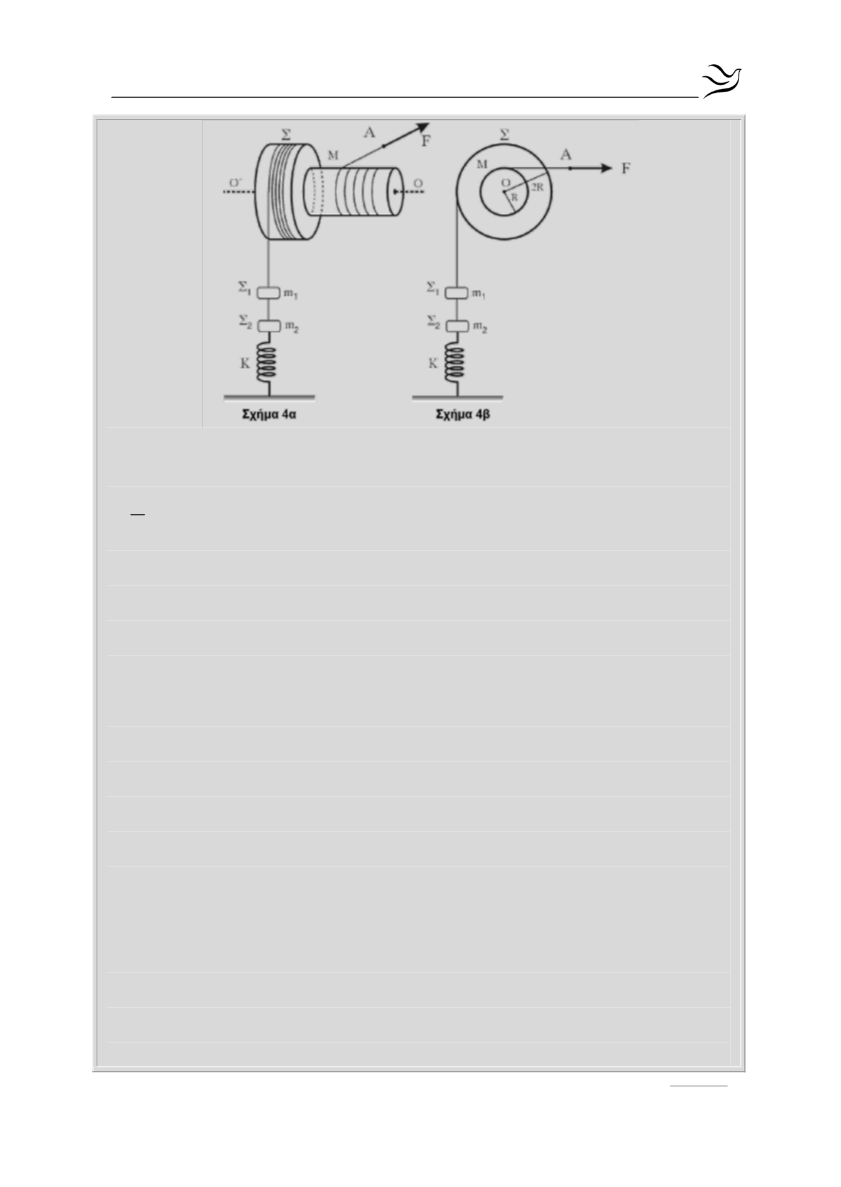
Η ροπή αδράνειας του στερεού Σ ως προς τον άξονα περιστροφής του είναι
2
= ΜR
3
I
2
. Το στερεό Σ μπορεί να περιστρέφεται χωρίς τριβές γύρω από
σταθερό οριζόντιο άξονα Ο΄Ο. Ο οριζόντιος άξονας περιστροφής συμπίπτει με
τον άξονα συμμετρίας του κυλίνδρου. Γύρω από τον κύλινδρο του στερεού
ακτίνας R είναι τυλιγμένο πολλές φορές αβαρές μη εκτατό νήμα μεγάλου
μήκους, στο ελεύθερο άκρο Α του οποίου ασκείται οριζόντια δύναμη μέτρου
F=100N.
Στο ελεύθερο άκρο αβαρούς μη εκτατού νήματος μεγάλου μήκους, που είναι
τυλιγμένο στον κύλινδρο ακτίνας 2R, είναι δεμένο σώμα Σ
1
μάζας m
1
=2kg. Το
σώμα Σ
1
συνδέεται με αβαρές μη εκτατό νήμα με σώμα Σ
2
μάζας m
2
=1kg, που
συγκρατείται στερεωμένο σε κατακόρυφο ελατήριο σταθεράς Κ.
Το σύστημα του στερεού Σ και των σωμάτων Σ
1
και Σ
2
αρχικά ισορροπεί, με το
ελατήριο να έχει επιμηκυνθεί κατά Δℓ=0,2m από το φυσικό του μήκος. Τη
χρονική στιγμή μηδέν (t
0
=0s) το νήμα που συνδέει τα σώματα Σ
1
και Σ
2
κόβεται.
Το σώμα Σ
2
αρχίζει να εκτελεί απλή αρμονική ταλάντωση, ενώ το στερεό Σ
αρχίζει να περιστρέφεται γύρω από τον οριζόντιο άξονα περιστροφής του Ο΄Ο.
Δ1. Να υπολογίσετε την τιμή της σταθεράς Κ του ελατηρίου.









