Εκδόσεις ΜΠΑΧΑΡΑΚΗ –
Φυσική Ομάδας Προσανατολισμού Θετικών Σπουδών
50
Ομογενής δίσκος Σ
1
έχει μάζα Μ
1
=8kg και ακτίνα R
1
=0,2m. Στο σημείο Β της
κατακόρυφης διαμέτρου του δίσκου, που απέχει απόσταση d=
3
2
R από το
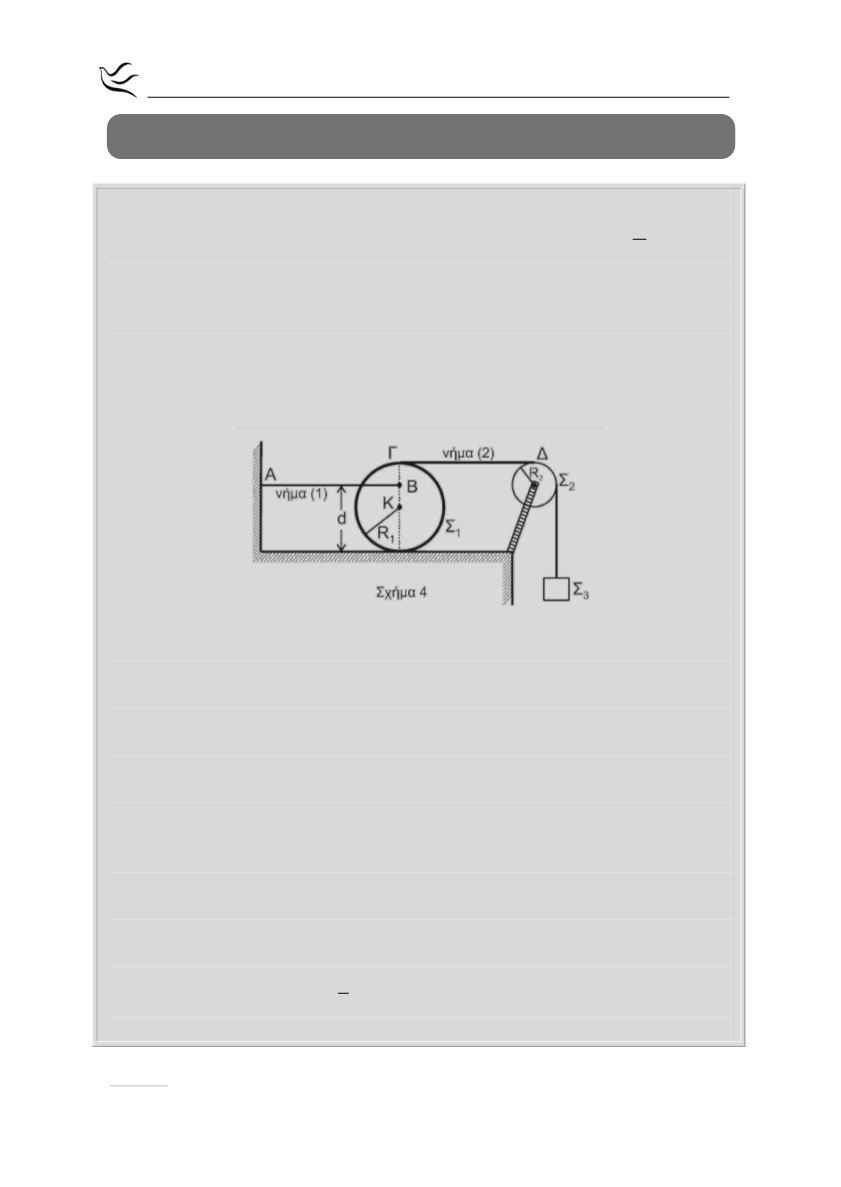
οριζόντιο επίπεδο, είναι στερεωμένο οριζόντιο αβαρές μη εκτατό νήμα (1).
Το άλλο άκρο Α του νήματος (1) είναι ακλόνητα στερεωμένο, όπως φαίνεται
στο σχήμα 4. Γύρω από την περιφέρεια του δίσκου Σ
1
είναι τυλιγμένο πολλές
φορές άλλο δεύτερο αβαρές μη εκτατό νήμα (2), το οποίο διέρχεται από
τροχαλία Σ
2
, μάζας Μ
2
=2kg και ακτίνας R
2
=0,1m. Στο άλλο άκρο του νήματος
(2) είναι συνδεδεμένο σώμα Σ
3
, μάζας Μ
3
=1kg. Το σύστημα αρχικά ισορροπεί.
Το τμήμα ΓΔ του νήματος (2) είναι οριζόντιο.
Δ1. Να υπολογίσετε το μέτρο της τάσης που ασκεί το νήμα (1) στο δίσκο Σ
1
.
Μονάδες 6
Τη χρονική στιγμή t
0
=0 το νήμα (1) κόβεται. Το σώμα Σ
3
κατέρχεται με
επιτάχυνση. Η τροχαλία Σ
2
αρχίζει να περιστρέφεται, χωρίς τριβές, γύρω από
τον άξονά της και ο δίσκος Σ
1
αρχίζει να κυλίεται, χωρίς να ολισθαίνει, πάνω
στο οριζόντιο επίπεδο.
Δ2. Να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του δίσκου
Σ
1
. Μονάδες 10
Δ3. Να υπολογίσετε το μέτρο της στροφορμής της τροχαλίας Σ
2
τη χρονική
στιγμή t
1
= 1s. Μονάδες 5
Δ4. Να υπολογίσετε τη μεταβολή της βαρυτικής δυναμικής ενέργειας του
σώματος Σ
3
για την κίνηση του από τη χρονική στιγμή t
0
=0 έως τη χρονική
στιγμή t
1
=1s. Μονάδες 4
Δίνονται: η επιτάχυνση της βαρύτητας g=10m/s
2
.
η ροπή αδρανείας του δίσκου ως προς τον άξονα περιστροφής που διέρχεται
από το κέντρο μάζας του
1 2
I = Μ R
1 1 1 2
η ροπή αδρανείας της τροχαλίας ως προς τον άξονα περιστροφής που
ΘΕΜΑ Δ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2016









