203
ΑΕΠΠ – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
δεδομένα, λοιπόν, που βρίσκονται στην κορυφή της στοίβας λαμβάνονται
πρώτα, ενώ αυτά που βρίσκονται στο βάθος της στοίβας λαμβάνονται τελευταία.
Αυτή η μέθοδος επεξεργασίας ονομάζεται τελευταίο μέσα, πρώτο έξω ή
απλούστερα με την αγγλική συντομογραφία LIFO (Last-In-First-Out). Δύο είναι οι
κύριες λειτουργίες σε μία στοίβα:
→
Η ώθηση (push) στοιχείου στην κορυφή της στοίβας, και
→
Η απώθηση (pop) στοιχείου από τη στοίβα.
Η διαδικασία της ώθησης πρέπει οπωσδήποτε να ελέγχει, αν η στοίβα είναι
γεμάτη, οπότε λέγεται ότι συμβαίνει υπερχείλιση (overflow) της στοίβας.
Αντίστοιχα, η διαδικασία απώθησης ελέγχει, αν υπάρχει ένα τουλάχιστον
στοιχείο στη στοίβα, δηλαδή ελέγχει αν γίνεται υποχείλιση (underflow) της
στοίβας. Μια στοίβα μπορεί να υλοποιηθεί πολύ εύκολα με τη βοήθεια ενός
μονοδιάστατου πίνακα. Μια βοηθητική μεταβλητή (με όνομα συνήθως top)
χρησιμοποιείται για να δείχνει τη θέση του στοιχείου που τοποθετήθηκε
τελευταίο στην κορυφή της στοίβας. Για την εισαγωγή ενός νέου στοιχείου στη
στοίβα (ώθηση) αρκεί να αυξηθεί η μεταβλητή top κατά ένα και στη θέση αυτή
να εισέλθει το στοιχείο. Αντίθετα για την εξαγωγή ενός στοιχείου από τη στοίβα
(απώθηση) εξέρχεται πρώτα το στοιχείο που δείχνει η μεταβλητή top και στη
συνέχεια η top μειώνεται κατά ένα για να δείχνει τη νέα κορυφή.
Δ.
Να γράψετε τις παρακάτω μαθηματικές εκφράσεις σε «ΓΛΩΣΣΑ»
1.
2
x ημθ
x 5
−
+
(Μονάδες 2)
2.
(
)
x
2
3 x 1
2x+
e
y 1
+
−
+
(Μονάδες 2)
Απάντηση:
Δ.
Οι εκφράσεις σε γλώσσα είναι:
1.
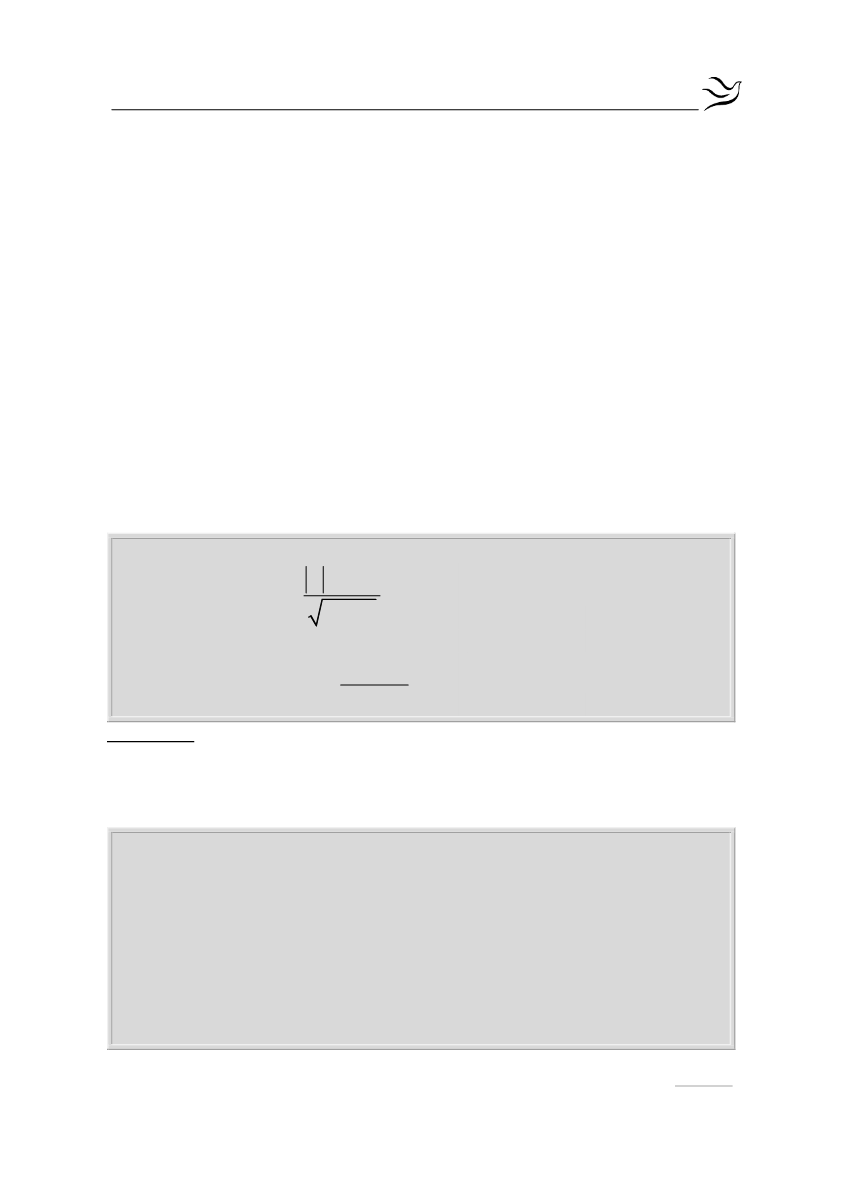
(Α_Τ(x)-HM(θ) )/ (Τ_Ρ( x^2+5))
2.
2*x+ (3*( x+1))/ y^2+1)-E(x)
Ε.
Δίνεται το παρακάτω τμήμα αλγορίθμου:
Κ ← 1
ΓΙΑ
i
ΑΠΟ
-1
ΜΕΧΡ
Ι -5
ΜΕ_ΒΗΜΑ
-2
Κ ← Κ * i
ΓΡΑΨΕ
Κ
ΤΕΛΟΣ_ ΕΠΑΝΑΛΗΨΗΣ
Να μετατρέψετε το τμήμα αυτού του αλγορίθμου σε ισοδύναμο:
α.
με χρήση της αλγοριθμικής δομής
ΟΣΟ
(Μονάδες 3)
β.
με χρήση της αλγοριθμικής δομής
ΜΕΧΡΙΣ_ΟΤΟΥ
(Μονάδες 3)









